Astrocytes enhance plasticity response during reversal learning

7 minute read see also thread comments

↑

Astrocytes, a type of glial cell traditionally considered support cells in the brain, are now recognized as active participants in synaptic plasticity and memory. I found this development particularly compelling and presented the following study in our Journal Club. The paper by Squadrani et al. (2024)ꜛ explores the role of astrocyte-mediated D-serine regulation in modulating learning flexibility, particularly during reversal learning — the ability to adapt to changes in the environment. The work builds on prior experiments by Bohmbach et al. (2022)ꜛ, which identified an astrocyte-neuron feedback loop involving endocannabinoids and astrocytic D-serine release in the hippocampus.

The role of astrocytes in synaptic plasticity

Synaptic plasticity, the ability of synapses to strengthen or weaken over time, is fundamental to learning and memory. Historically, plasticity research was almost exclusively neuron-centric. However, astrocytes — once considered passive — are now understood to regulate neurotransmission and plasticity, notably through the release of D-serine, a co-agonist at NMDA receptors.

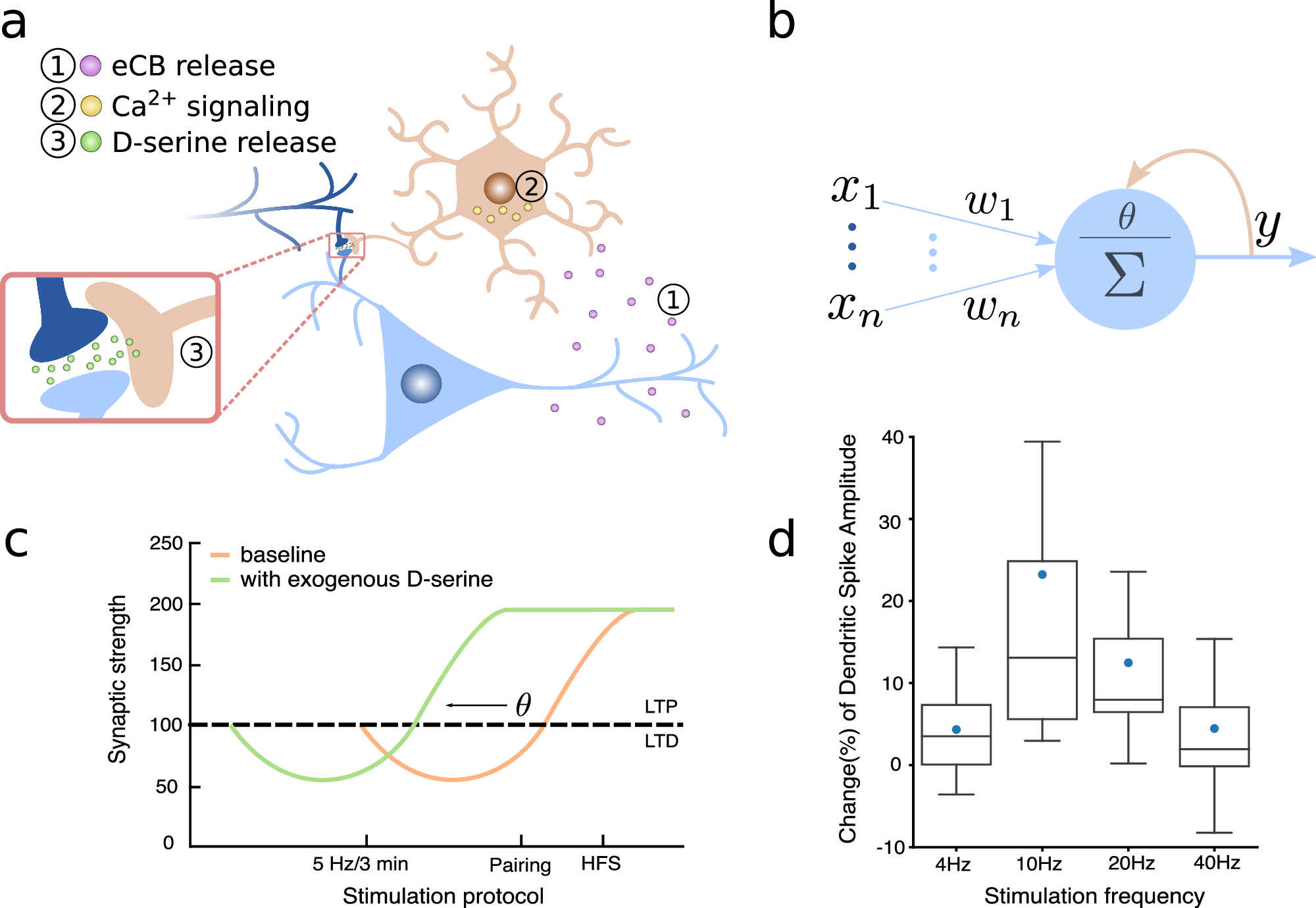
Fig. 1 from Squadrani et al. (2024): The D-serine hypothesis.
Fig. 1 from Squadrani et al. (2024)ꜛ: The D-serine hypothesis. Astrocyte-mediated feedback loop involving endocannabinoids and D-serine, showing similarity to the dynamic threshold postulated in the BCM theory. Panel d illustrates the bell-shaped relationship between D-serine levels and stimulation frequency. Source: Communications Biology (Commun Biol)ꜛ (license: Creative Commons Attribution 4.0 International License)

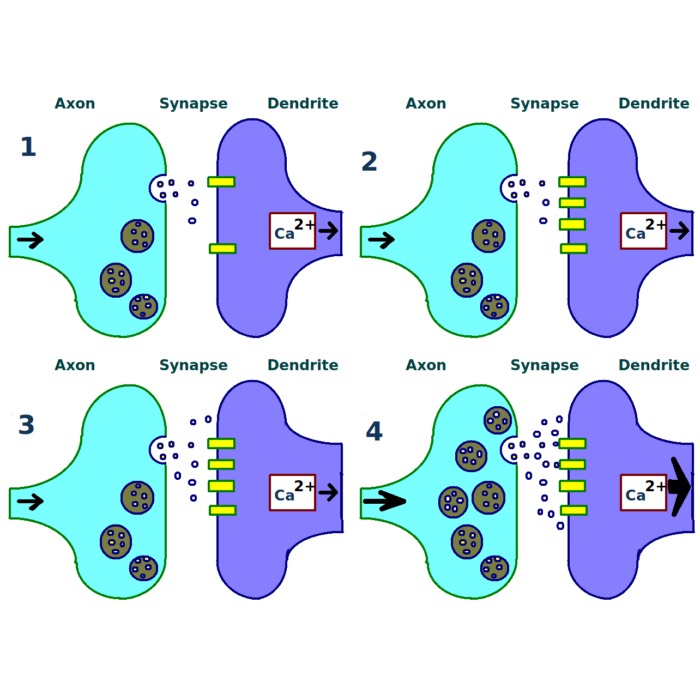
The astrocytic D-serine pathway plays a particularly interesting role: neuronal activity triggers endocannabinoid release, which activates astrocytic CB1 receptors, leading to D-serine release in a calcium-dependent manner. This extracellular D-serine level in turn modulates NMDA receptor activation — effectively influencing whether long-term potentiation (LTP) or long-term depression (LTD) occurs.

Key findings and hypotheses

The central hypothesis of the paperꜛ — referred to as the D-serine hypothesis — is that astrocytic D-serine regulation provides a biophysical mechanism for the dynamic threshold postulated in the BCM (Bienenstock–Cooper–Munro) theory of synaptic plasticity. Specifically:

  • Astrocytic feedback loop: Astrocytes release D-serine in a non-monotonic, bell-shaped response to post-synaptic activity, peaking at moderate firing rates. This modulates the induction threshold for LTP.
  • Learning behavior: Mice with genetically disrupted astrocytic D-serine signaling (via CB1 receptor knockout in astrocytes) showed normal initial learning, but impaired performance during reversal learning.
  • Modeling insight: A mathematically formalized model incorporating D-serine dynamics reproduces both the normal and impaired behavioral results and aligns with the classical BCM formulation.

Experimental design and results

The behavioral task used was a place avoidance paradigm in an O-shaped maze. Mice learned to avoid a location where they received an aversive air puff. After successful learning, the location of the stimulus was reversed to test adaptation.

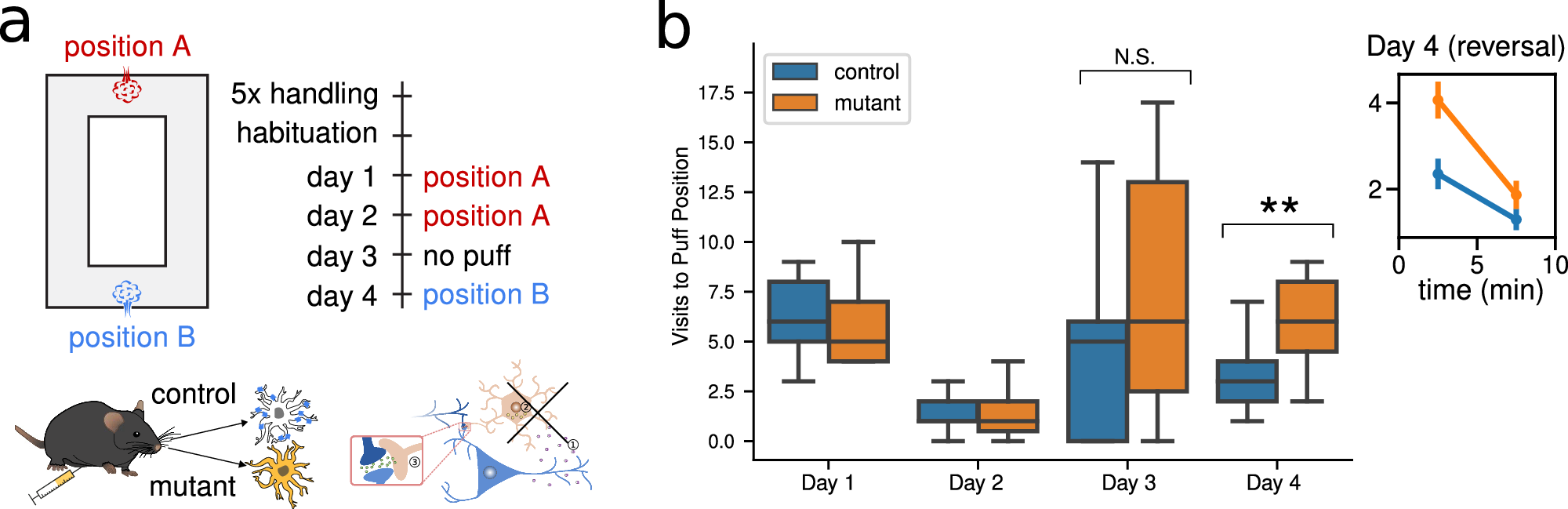
Fig. 2 from Squadrani et al. (2024): Learning impairment of mutant mice during a place-avoidance.
Fig. 2 from Squadrani et al. (2024)ꜛ: Learning impairment of mutant mice during a place-avoidance. Behavioral assay for reversal learning using a place avoidance task in a ring-shaped maze. Mutant mice lacking astrocytic CB1 receptors show normal initial learning but significantly impaired reversal learning (Day 4). Source: Communications Biology (Commun Biol)ꜛ (license: Creative Commons Attribution 4.0 International License)

Findings:

  • Control mice: Learned both phases (initial and reversal) effectively.
  • Mutant mice: Learned the first association normally, but showed a clear deficit in reversal learning — adapting more slowly to the new contingency.

This behavioral difference was not general, but specific to flexibility — a hallmark of adaptive plasticity.

Mathematical framework

The authors developed a biophysical model based on astrocytic D-serine dynamics, extending the classic BCM rule.

D-serine dynamics:
Let $\nu$ be the average post-synaptic firing rate, and $d$ the D-serine concentration. The D-serine concentration follows:

\[\tau_d \frac{d}{dt}d = -d + D(\nu)\]

where $\tau_d$ is a time constant, and $D(\nu)$ is a function of the post-synaptic activity given by:

\[D(\nu) = D_0 - a(\nu - \nu_0)^2\]

Here, $D_0$ is the maximum D-serine concentration, $\nu_0$ is the optimal firing rate, and $a$ is a constant.

This implements a bell-shaped dependence on $\nu$, with maximum D-serine at $\nu_0$.

BCM-like weight update: The synaptic weight update rule is defined by:

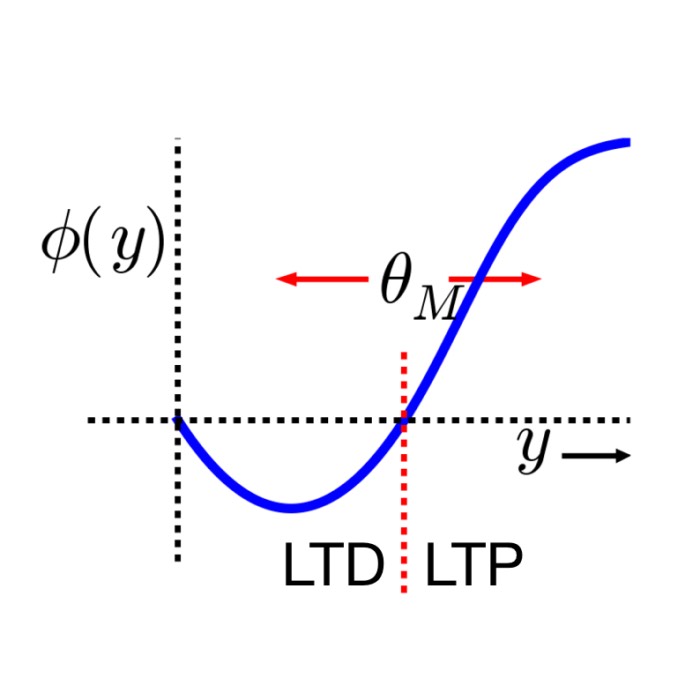
\[\tau_w \frac{dw}{dt} = xy (y - \theta(d))\]

where $\tau_w$ is a time constant, $x$ and $y$ are pre- and post-synaptic activities, respectively, and $\theta(d)$ is the dynamic threshold:

\[\theta(d) = b (D_0 - d)\]

with $b$ being a constant.

Thus, the LTP threshold $\theta$ is not postulated but derived from extracellular D-serine levels.

Reinforcement extension (R-BCM):
To model behavioral learning with punishment, a reinforcement-modulated plasticity rule was introduced:

\[\Delta w_t = -R(S_{t+1}) x_t y_t (y_t - \theta_t)\]

where $R(S_{t+1})$ is the reinforcement signal associated with the next state $S_{t+1}$.

This allows the system to learn state-value associations and adapt behaviorally.

Task modeling:
A two-state model ($S_1$, $S_2$) with state-switching probability $p_{\text{change}} = \max(0.05, y_t)$ was used to simulate the place avoidance task.

Fig. 3 from Squadrani et al. (2024): Simulation of the passive place-avoidance task.
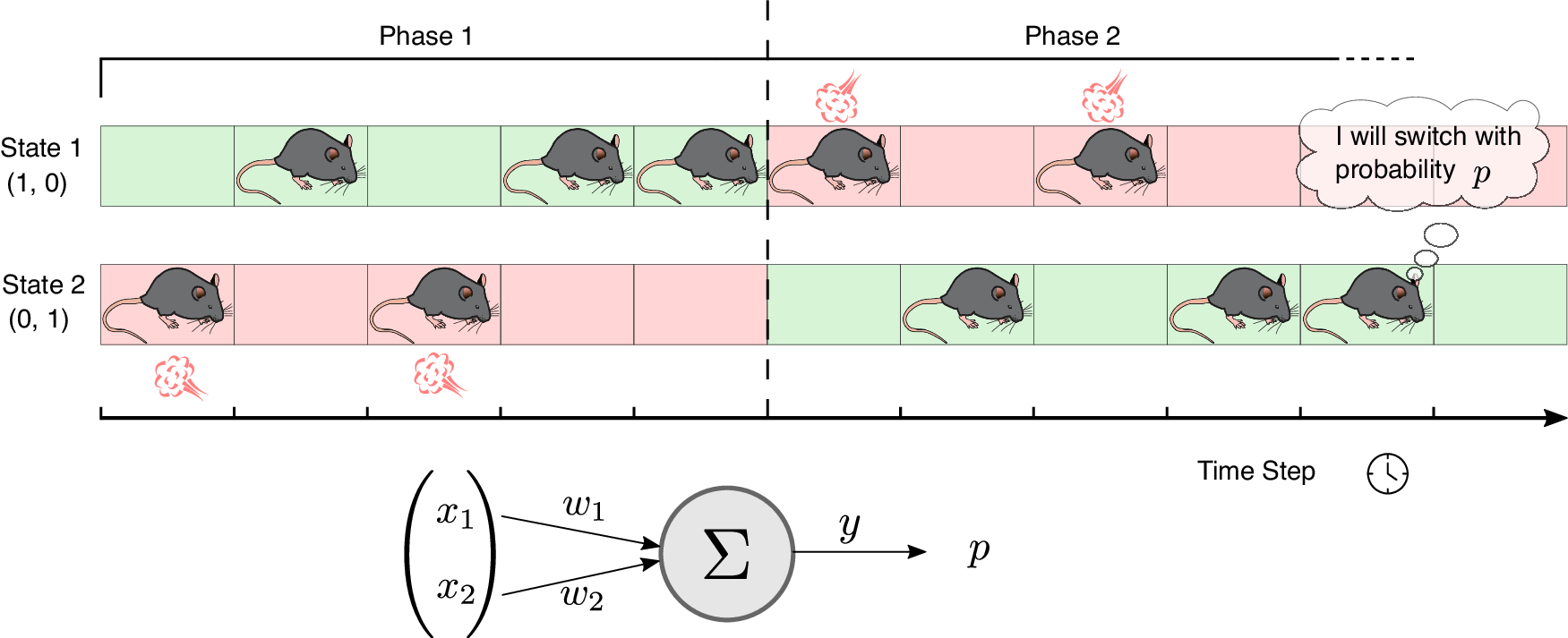
Fig. 3 from Squadrani et al. (2024)ꜛ: Simulation of the passive place-avoidance task. Behavioral assay for reversal learning using a place avoidance task in a ring-shaped maze. Simplified two-state model used in simulations. The agent learns to avoid punishment based on the synaptic weights of a single action unit updated via BCM-like plasticity. Source: Communications Biology (Commun Biol)ꜛ (license: Creative Commons Attribution 4.0 International License)

Stability analysis:
The system’s stability is analyzed by solving the stationary points:

\[\begin{align*} E[\Delta w] =& -p_1 x_1 (p_{11} R_1 + p_{21} R_2) y_1 (y_1 - \theta) \\ & - p_2 x_2 (p_{22} R_2 + p_{12} R_1) y_2 (y_2 - \theta) = 0 \end{align*}\]

The eigenvector corresponding to the eigenvalue 1 of the transition matrix $\Pi$ gives the stationary distribution:

\[\Pi = \begin{pmatrix} 1 - p_{\text{change}}(y_1) & p_{\text{change}}(y_2) \\ p_{\text{change}}(y_1) & 1 - p_{\text{change}}(y_2) \end{pmatrix}\]

where $y_i = w \cdot x_i$.

This shift in model dynamics is critical: without activity-dependent D-serine regulation, the system loses its ability to flexibly adjust the plasticity threshold, a mechanism essential for adapting to environmental changes. Notably, the disruption of D-serine dynamics led to a fixed LTP threshold, preventing rapid adaptation during reversal — matching the experimental phenotype.

Model results and predictions

The simulations reproduce the behavioral asymmetry seen in mice:

  • In Phase 1, both control and mutant agents learned to avoid the punished location.
  • In Phase 2 (reversal), only control agents adapted quickly.
  • In mutants, learning was slower due to the lack of D-serine modulation, which normally lowers the LTP threshold during changing contingencies.

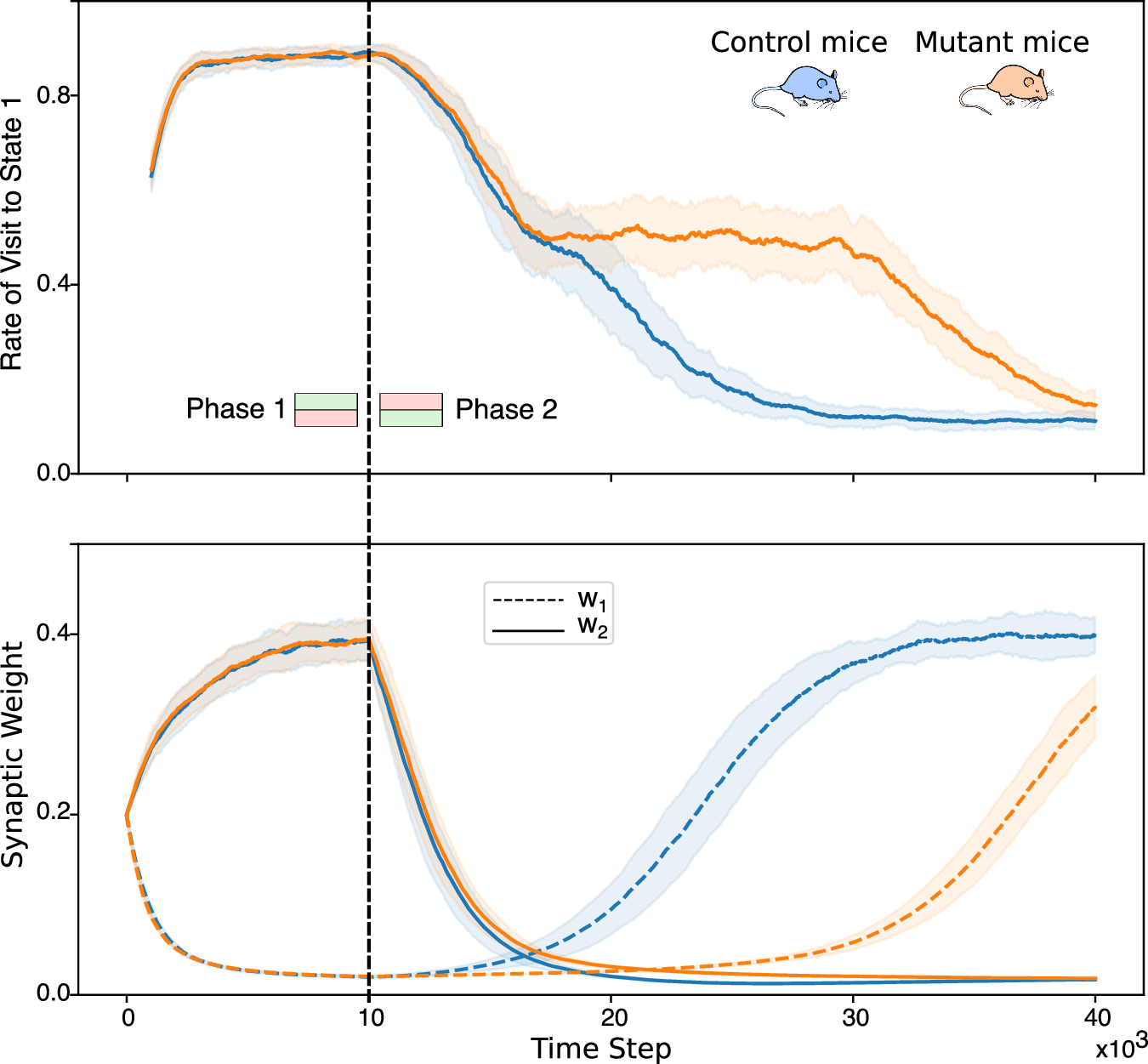
Fig. 4 from Squadrani et al. (2024): Simulation of the passive place-avoidance task.
Fig. 4 from Squadrani et al. (2024)ꜛ: The model reproduces learning deficit in mutant mice. Top: State visit frequency over time. Bottom: Corresponding synaptic weight evolution for control and mutant simulations. Source: Communications Biology (Commun Biol)ꜛ (license: Creative Commons Attribution 4.0 International License)

Moreover, increased D-serine levels during reversal learning are predicted by the model and could be tested experimentally (cf. Fig. 5 in the paper). The model also shows that enhancing punishment (increasing $|R|$) can partially compensate for the loss of D-serine regulation in mutants.

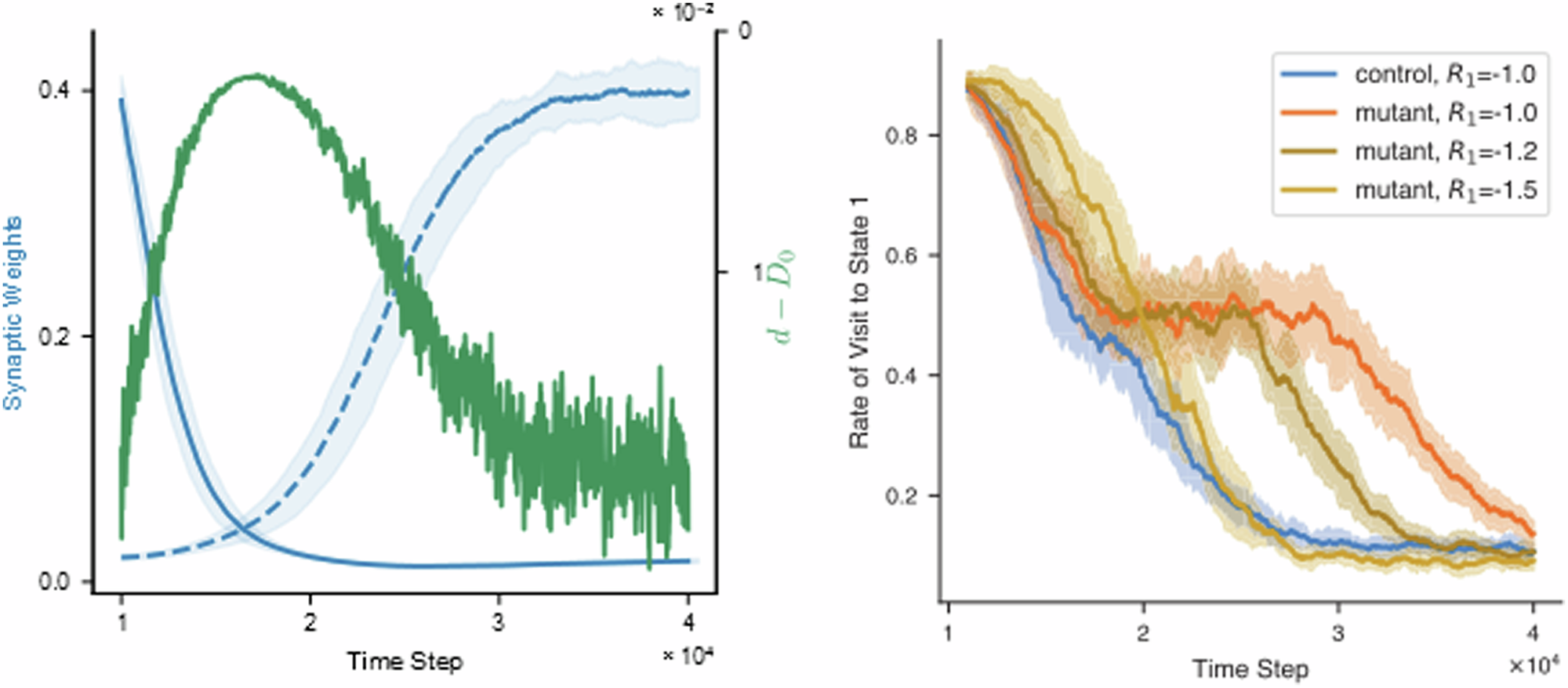
Fig. 5 from Squadrani et al. (2024): Simulation of the passive place-avoidance task.
Fig. 5 from Squadrani et al. (2024)ꜛ. Left: D-serine levels increase during reversal learning in control simulations, reducing the LTP threshold. Right: Increasing punishment strength restores learning in mutant models. Source: Communications Biology (Commun Biol)ꜛ (license: Creative Commons Attribution 4.0 International License)

Discussion and Implications

This work bridges experimental neurobiology and theoretical modeling by grounding the BCM plasticity rule in a biophysical astrocytic mechanism. It proposes:

  • Astrocytic D-serine as a regulator of LTP thresholds, enabling fast learning adjustments.
  • A reinforcement-compatible plasticity rule (R-BCM) that models behavioral adaptation.
  • A testable prediction: extracellular D-serine should transiently increase during reversal learning in healthy animals.

It also raises key mechanistic questions:

  • Could astrocytic modulation be synapse-specific, rather than neuron-wide as BCM assumes?
  • How does D-serine influence STDP windows and higher-order spike interactions?
  • Can this mechanism stabilize networks in the absence of external reinforcement?

Conclusion

Squadrani et al. (2024)ꜛ offer an elegant and plausible mechanism connecting glial biology with learning theory. Their study shows that astrocytes — via D-serine — do more than support neurons: they regulate when and how neurons change. By translating this into a computational model, they not only explain a specific behavioral deficit but also open the way for a deeper understanding of plasticity regulation — one that includes the long-neglected but essential glial partners.

2 other articles are linked to this site

Bienenstock-Cooper-Munro (BCM) rule

15 minute read

The Bienenstock-Cooper-Munro (BCM) rule is a cornerstone in theoretical neuroscience, offering a comprehensive framework f...

Related posts

Bienenstock-Cooper-Munro (BCM) rule

15 minute read

The Bienenstock-Cooper-Munro (BCM) rule is a cornerstone in theoretical neuroscience, offering a comprehensive framework f...

Frequency-current (f-I) curves

6 minute read

In this short tutorial, we will explore the concept of frequency-current (f-I) curves exemplified by the Hodgkin-Huxley ne...

comments