Blog posts by Tag
- Cheat Sheets 12
- Computational Science 38
- Data Science 67
- Image Processing 9
- Independent Web 11
- Jekyll 13
- Machine Learning/AI 28
- Markdown/LaTeX 30
- Neuroscience 40
- Open Source 52
- Personal Knowledge Management 19
- Personal Opinion 14
- Photography 1
- Physics 3
- Privacy 3
- Python 96
- Scientific Writing 28
- Teaching 19
- Web Design 18
#Cheat Sheets (12)
Hacks and extensions to improve your coding with Visual Studio Code
This curated list contains useful hacks and extensions to improve the overall coding performance with Visual Studio Code (VS Code).
New Teaching Material: Python Cheat Sheets
I’ve started a collection of various Python cheat sheets that contain some useful and commonly used commands and usage examples.
Dealing with future posts in Jekyll
While drafting blog posts in Jekyll, you may want to keep some posts hidden from the public eye until they’re ready to be published. In the world of blogging with Jekyll, there are several effective methods to draft such posts without immediately publishing them. Here are three practical approaches.
Running and testing your Jekyll site locally with custom options
Developing with Jekyll often requires running your site locally to test changes before deploying them live. Here is a handy yet useful one-line command that I usually use to run my Jekyll site locally with custom options.
strftime Cheat Sheet
Cheat Sheet on formatted date and time strings used, e.g., in Python, C/C++ or even on Jekyll websites by using Liquid tags.
Liquid Cheat Sheet
This Cheat Sheet gives an overview of Liquid syntax commands one might encounter while developing a Jekyll website.
Minimal Mistakes Cheat Sheet
A quick overview of available commands for creating content with the Minimal Mistakes Jekyll theme.
New Teaching Material: LaTeX Guide
I’ve added a LaTeX guide to the General Teaching Materials in the teaching section. It serves as a Getting started with LaTeX guide and as a LaTeX glossary.
#Computational Science (38)
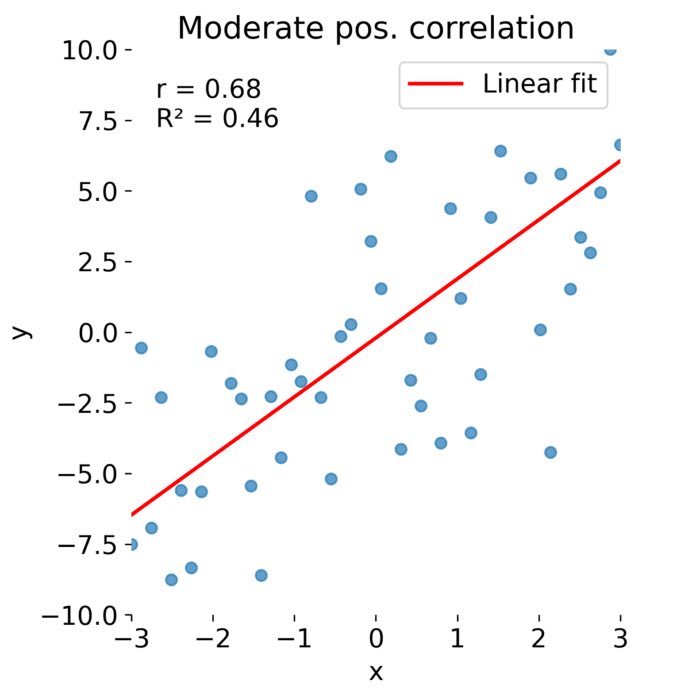
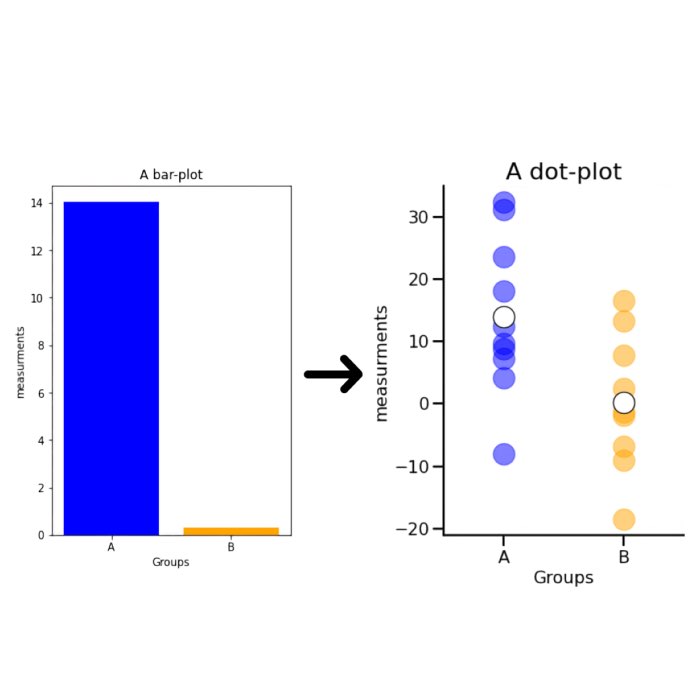
Distinguishing correlation from the coefficient of determination: Proper reporting of r and R²
I noticed that people sometimes report R² (‘R-squared’) instead of the Pearson correlation coefficient r when discussing the correlation between two variables. In the special case of a simple linear relationship this numerical equality is not strictly wrong, yet presenting R² as if it were the correlation coefficient might wrongly give the impression they are the same thing. In this post, we will therefore unpack the difference between these two measures, explain their mathematical definitions and proper usage discuss the best practices for when to use each in statistical reporting.
Rate models as a tool for studying collective neural activity
Rate models provide simplified representations of neural activity in which the precise spike timing of individual neurons is replaced by their average firing rate. This abstraction makes it possible to study the collective behavior of large neuronal populations and to analyze network dynamics in a tractable way. I recently played around with some rate models in Python, and in this post I’d like to share what I have learned so far about their implementation and utility.
On the role of gap junctions in neural modelling: Network example
As a follow-up to our previous post on gap junctions, we will now explore how gap junctions can be implemented in a network of spiking neurons (SNN) using the NEST simulator. Gap junctions are electrical synapses that allow direct electrical communication between neurons, which can significantly influence the dynamics of neural networks.
On the role of gap junctions in neural modelling
Gap junctions are specialized intercellular connections that facilitate direct electrical and chemical communication between neurons. Unlike synaptic transmission, which involves neurotransmitter release, gap junctions enable the direct passage of ions and small molecules through channels formed by connexins, leading to synchronized neuronal activity. In computational neuroscience, modeling gap junctions is crucial for understanding their role in neural network dynamics, synchronization, and various brain functions.
Shared dynamics, diverse responses: decoding decision-making in premotor cortex
Last week, I presented a recent study by Genkin et al., The dynamics and geometry of choice in the premotor cortex, in our Journal Club, and I found it conceptually compelling enough to summarize it here as well. The paper explores how perceptual decisions are encoded not in isolated neural responses but in population-wide latent dynamics. Traditionally, the neuroscience of decision-making has focused on ramping activity in individual neurons, heterogeneous peristimulus time histograms (PSTHs), and decoding strategies based on trial-averaged firing rates. In contrast, this work proposes that a shared low-dimensional decision variable evolves over time and explains the observed diversity in single-neuron responses. In our discussion, we focused on the paper’s central figures, using them to guide a step-by-step reconstruction of the study’s logic and findings.
Astrocytes enhance plasticity response during reversal learning
Astrocytes, a type of glial cell traditionally considered support cells in the brain, are now recognized as active participants in synaptic plasticity and memory. I found this development particularly compelling and presented the following study in our Journal Club. The paper by Squadrani et al. (2024) explores the role of astrocyte-mediated D-serine regulation in modulating learning flexibility, particularly during reversal learning — the ability to adapt to changes in the environment. The work builds on prior experiments by Bohmbach et al. (2022), which identified an astrocyte-neuron feedback loop involving endocannabinoids and astrocytic D-serine release in the hippocampus.
New teaching material: Dimensionality reduction in neuroscience
We just completed a new two-day course on Dimensionality Reduction in Neuroscience, and I am pleased to announce that the full teaching material is now freely available under a Creative Commons (CC BY 4.0) license. This course is designed to provide an introductory overview of the application of dimensionality reduction techniques for neuroscientists and data scientists alike, focusing on how to handle the increasingly high-dimensional datasets generated by modern neuroscience research.
Long-term potentiation (LTP) and long-term depression (LTD)
Both long-term potentiation (LTP) and long-term depression (LTD) are forms of synaptic plasticity, which refers to the ability of synapses to change their strength over time. These processes are crucial for learning and memory, as they allow the brain to adapt to new information and experiences. Since we are often talking about both processes in the context of computational neuroscience, I thought it would be useful to provide a brief overview of biological mechanisms underlying these processes and their significance in the brain.
Bienenstock-Cooper-Munro (BCM) rule
The Bienenstock-Cooper-Munro (BCM) rule is a cornerstone in theoretical neuroscience, offering a comprehensive framework for understanding synaptic plasticity – the process by which connections between neurons are strengthened or weakened over time. Since its introduction in 1982, the BCM rule has provided critical insights into the mechanisms of learning and memory formation in the brain. In this post, we briefly explore and discuss the BCM rule, its theoretical foundations, mathematical formulations, and implications for neural plasticity.
Campbell and Siegert approximation for estimating the firing rate of a neuron
The Campbell and Siegert approximation is a method used in computational neuroscience to estimate the firing rate of a neuron given a certain input. This approximation is particularly useful for analyzing the firing behavior of neurons that follow a leaky integrate-and-fire (LIF) model or similar models under the influence of stochastic input currents.
Exponential (EIF) and adaptive exponential Integrate-and-Fire (AdEx) model
The exponential Integrate-and-Fire (EIF) model is a simplified neuronal model that captures the essential dynamics of action potential generation. It extends the classical Integrate-and-Fire (IF) model by incorporating an exponential term to model the rapid rise of the membrane potential during spike initiation more accurately. The adaptive exponential Integrate-and-Fire (AdEx) model is a variant of the EIF model that includes an adaptation current to account for spike-frequency adaptation observed in real neurons. In this tutorial, we will explore the key features of the EIF and AdEx models and their applications in simulating neuronal dynamics.
Olfactory processing via spike-time based computation
In their work ‘Simple Networks for Spike-Timing-Based Computation, with Application to Olfactory Processing’ from 2003, Brody and Hopfield proposed a simple network model for olfactory processing. Brody and Hopfield showed how networks of spiking neurons (SNN) can be used to process temporal information based on computations on the timing of spikes rather than the rate of spikes. This is particularly relevant in the context of olfactory processing, where the timing of spikes in the olfactory bulb is crucial for encoding odor information. In this tutorial, we recapitulate the main concepts of Brody and Hopfield’s network using the NEST simulator.
Frequency-current (f-I) curves
In this short tutorial, we will explore the concept of frequency-current (f-I) curves exemplified by the Hodgkin-Huxley neuron model. The f-I curve describes the relationship between the input current to a neuron and its firing rate. We will use the NEST simulator to simulate the behavior of a single Hodgkin-Huxley neuron and plot its f-I curve.
What are alpha-shaped post-synaptic currents?
In some recent posts, we have applied a specific type of integrate-and-fire neuron model, the
iaf_psc_alpha model implemented in the NEST simulator, to simulate the behavior of a single neuron or a population of neurons connected in a network. iaf_psc_alpha stands for ‘integrate-and-fire neuron with post-synaptic current shaped as an alpha function’. But what does ‘alpha-shaped current’ actually mean? In this short tutorial, we will explore the concept behind it.
Example of a neuron driven by an inhibitory and excitatory neuron population
In this tutorial, we recap the NEST tutorial ‘Balanced neuron example’. We will simulate a neuron driven by an inhibitory and excitatory population of neurons firing Poisson spike trains. The goal is to find the optimal rate for the inhibitory population that will drive the neuron to fire at the same rate as the excitatory population. This short tutorial is quite interesting as it is a practical demonstration of using the NEST simulator to model complex neuronal dynamics.
Brunel network: A comprehensive framework for studying neural network dynamics
In his work from 2000, Nicolas Brunel introduced a comprehensive framework for studying the dynamics of sparsely connected networks. The network is based on spiking neurons with random connectivity and differently balanced excitation and inhibition. It is characterized by a high level of sparseness and a low level of firing rates. The model is able to reproduce a wide range of neural dynamics, including both synchronized regular and asynchronous irregular activity as well as global oscillations. In this post, we summarize the essential concepts of that network and replicate the main results using the NEST simulator.
Oscillatory population dynamics of GIF neurons simulated with NEST
In this tutorial, we will explore the oscillatory population dynamics of generalized integrate-and-fire (GIF) neurons simulated with NEST. The GIF neuron model is a biophysically detailed model that captures the essential features of spiking neurons, including spike-frequency adaptation and dynamic threshold behavior. By simulating such a population of neurons, we can observe how these neurons interact and generate oscillatory firing patterns.
Izhikevich SNN simulated with NEST
In this post, we explore how easy it is to set up a large-scale, multi-population spiking neural network (SNN) with the NEST simulator. We simulate a simple SNN comprising two distinct populations of Izhikevich neurons, demonstrating the efficiency and flexibility of NEST and its capability to handle complex neural network simulations with ease.
Connection concepts in NEST
In the previous post, we learned about the basic concepts of the NEST simulator and how to create a simple single neuron model. This time, we will take a closer look at the connection concepts in NEST, which are crucial for building more complex neural networks.
Step-by-step NEST single neuron simulation
While NEST is designed for large-scale simulations of neural spike networks, the underlying models are based on approximating the behavior of single neurons and synapses. Before using NEST for network simulations, it is probably helpful to first understand the basic functions of the software tool by modelling and studying the behavior of individual neurons. In this tutorial, you will learn about NEST’s concept of nodes and connections, how to set up a neuron model of your choice, how to change model parameters, which different stimulation paradigms are included in NEST and how to record and analyze the simulation results.
NEST simulator – A powerful tool for simulating large-scale spiking neural networks
The NEST simulator is a powerful software tool designed for simulating large-scale networks of spiking neurons (SNN). It has become an essential instrument in the field of computational neuroscience, providing the capability to model, simulate, and analyze the complex dynamics of neuronal systems. And it comes with a user-friendly Python interface, facilitating the construction of neuronal networks with minimal effort.
Simulating spiking neural networks with Izhikevich neurons
The Izhikevich neuron model that we have discussed earlier is known for its simplicity and computational efficiency as well as for its biological plausibility. The model is based on two coupled differential equations that describe the membrane potential and the recovery variable of a neuron. The model can reproduce a wide range of spiking behaviors observed in real neurons, such as regular spiking, fast spiking, chattering, and more. In this post, we explore how we can quickly set up a spiking neural network (SNN) simulation using the Izhikevich neuron model in Python.
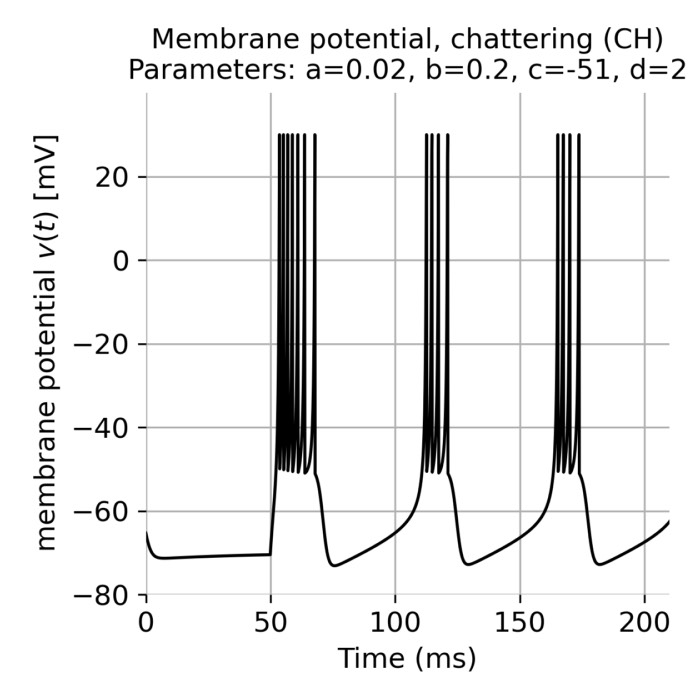
Izhikevich model
Computational neuroscience utilizes mathematical models to understand the complex dynamics of neuronal activity. Among various neuron models, the Izhikevich model stands out for its ability to combine biological fidelity with computational efficiency. Developed by Eugene Izhikevich in 2003, this model simulates the spiking and bursting behavior of neurons with a remarkable balance between simplicity and biological relevance. In this post, we explore the properties of the Izhikevich model, examining its application and adaptability in simulating single neuron behaviors.
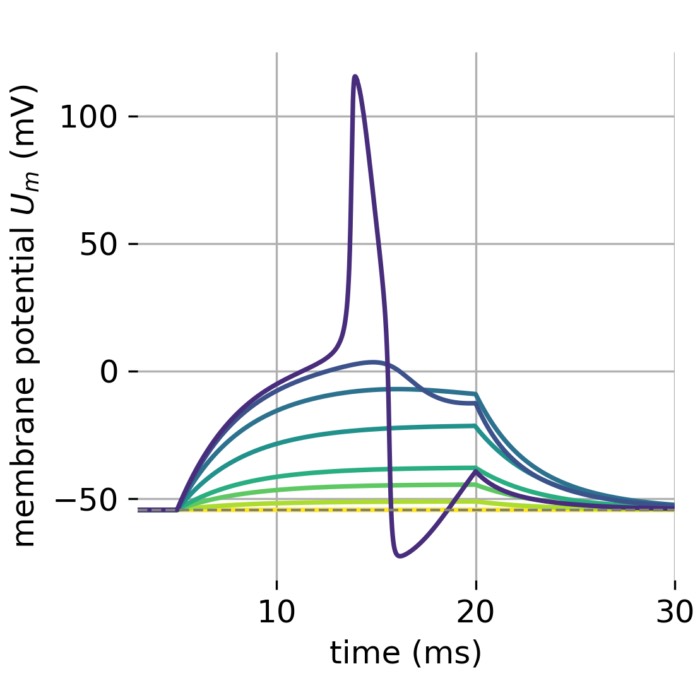
Hodgkin-Huxley model
An important step beyond simplified neuronal models is the Hodgkin-Huxley model. This model is based on the experimental data of Hodgkin and Huxley, who received the Nobel Prize in 1963 for their groundbreaking work. The model describes the dynamics of the membrane potential of a neuron by incorporating biophysiological properties instead of phenomenological descriptions. It is a cornerstone of computational neuroscience and has been used to study the dynamics of action potentials in neurons and the behavior of neural networks. In this post, we derive the Hodgkin-Huxley model step by step and provide a simple Python implementation.
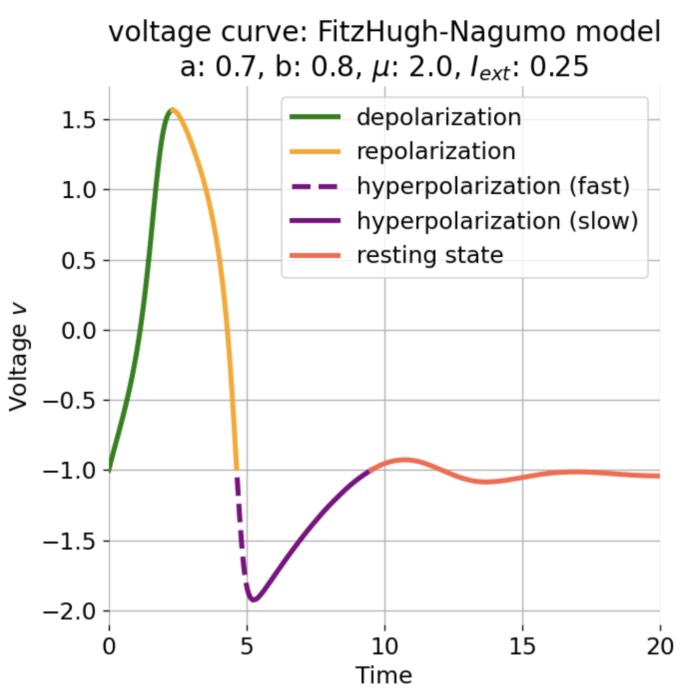
FitzHugh-Nagumo model
In the previous post, we analyzed the dynamics of Van der Pol oscillator by using phase plane analysis. In this post, we will see, that this oscillator can be considered as a special case of another dynamical system, the FitzHugh-Nagumo model. The FitzHugh-Nagumo model is a simplified model used to describe the dynamics of the action potential in neurons. With a few modifications of the Van der Pol equations we can obtain the model’s ODE system. By again using phase plane analysis, we can then investigate how the dynamics of the system changes under these modifications.
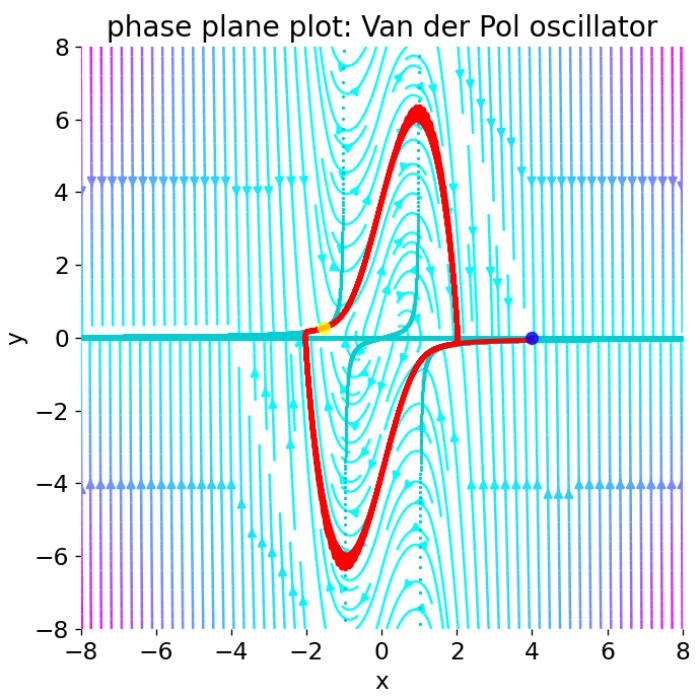
Van der Pol oscillator
In this post, we will apply phase plane analysis to the Van der Pol oscillator. The Van der Pol oscillator is a non-conservative oscillator with nonlinear damping, which was first described by the Dutch electrical engineer Balthasar van der Pol in 1920. We will explore how phase plane analysis can be used to gain insights into the behavior of this system and how it can be used to predict its long-term behavior.
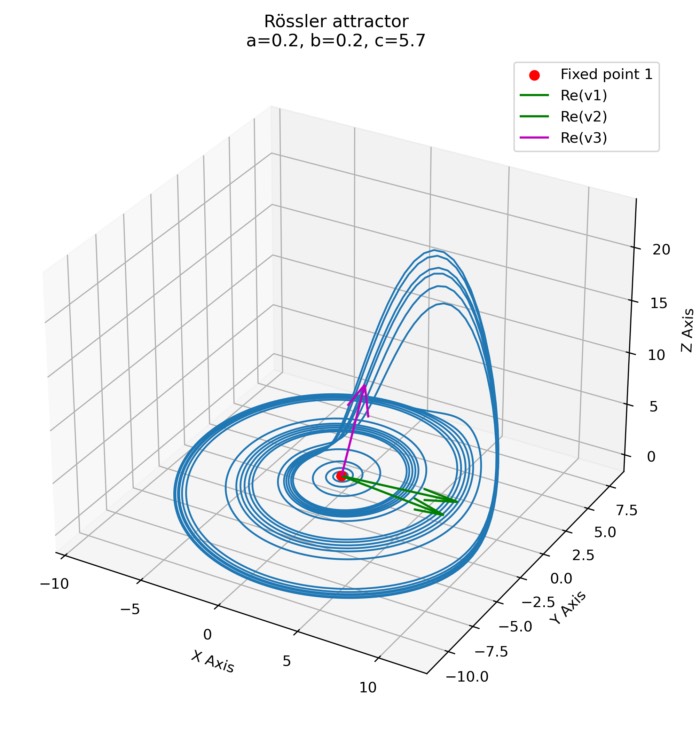
Nullclines and fixed points of the Rössler attractor
After introducing phase plane analysis in the previous post, we will now apply this method to the Rössler attractor presented earlier. We will investigate the system’s nullclines and fixed points, and analyze the attractor’s dynamics in the phase space.
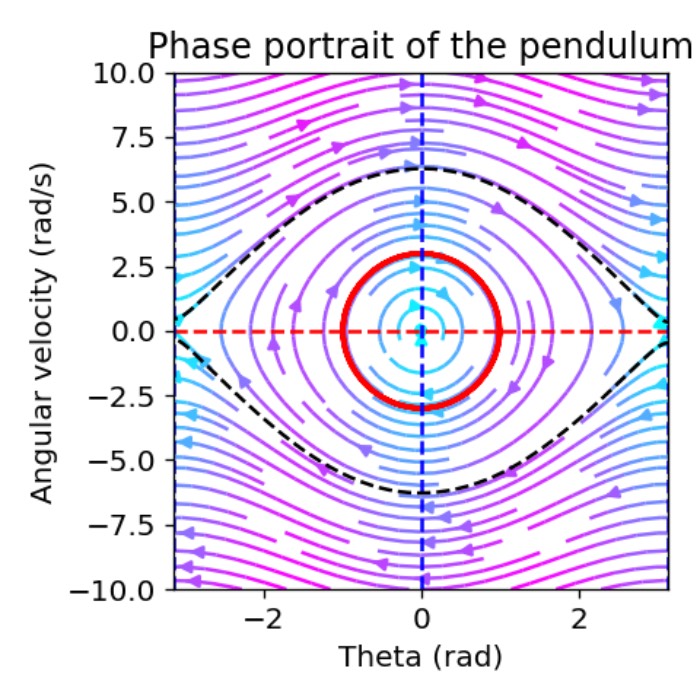
Using phase plane analysis to understand dynamical systems
When it comes to understanding the behavior of dynamical systems, it can quickly become too complex to analyze the system’s behavior directly from its differential equations. In such cases, phase plane analysis can be a powerful tool to gain insights into the system’s behavior. This method allows us to visualize the system’s dynamics in phase portraits, providing a clear and intuitive representation of the system’s behavior. Here, we explore how we can use this method and exemplarily apply it to the simple pendulum.
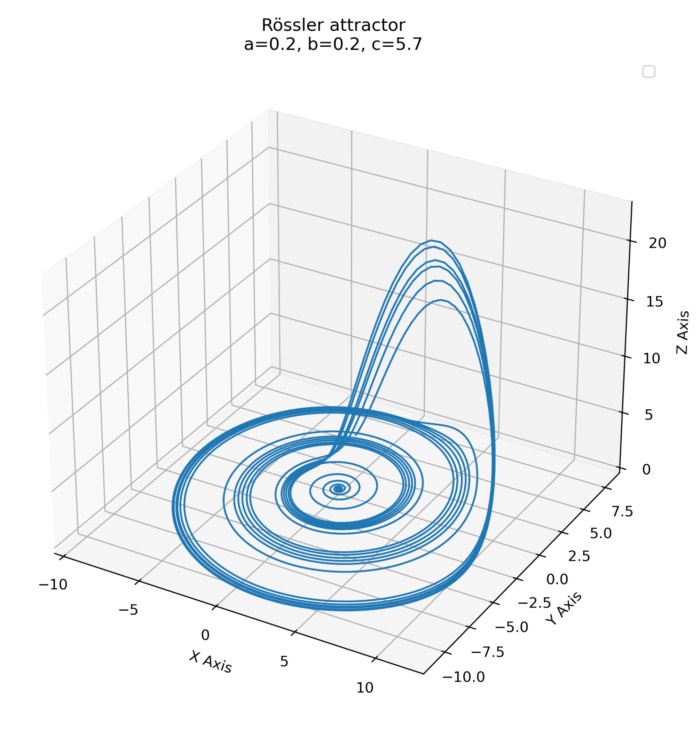
Rössler attractor
Unlike the Lorenz attractor which emerges from the dynamics of convection rolls, the Rössler attractor does not describe a physical system found in nature. Instead, it is a mathematical construction designed to illustrate and study the behavior of chaotic systems in a simpler, more accessible manner. In this post, we explore how we can quickly simulate this strange attractor using simple Python code.
Understanding Hebbian learning in Hopfield networks
Hopfield networks, a form of recurrent neural network (RNN), serve as a fundamental model for understanding associative memory and pattern recognition in computational neuroscience. Central to the operation of Hopfield networks is the Hebbian learning rule, an idea encapsulated by the maxim ‘neurons that fire together, wire together’. In this post, we explore the mathematical underpinnings of Hebbian learning within Hopfield networks, emphasizing its role in pattern recognition.
Building a neural network from scratch using NumPy
Ever thought about building you own neural network from scratch by simply using NumPy? In this post, we will do exactly that. We will build, from scratch, a simple feedforward neural network and train it on the MNIST dataset.
Integrate and Fire Model: A simple neuronal model
In this post we explore the Integrate-and-Fire model, a simplified representation of a neuron. We also run some simulations in Python to understand the model dynamics.
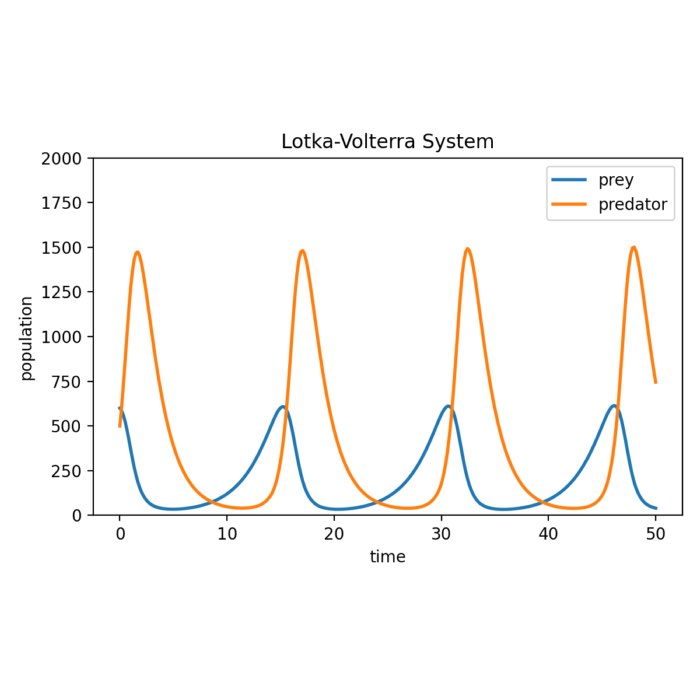
The Lotka-Volterra equations: Modeling predator-prey dynamics
The Lotka-Volterra system, also known as the predator-prey equations, is a mathematical model that describes the interaction between two species: predators and their prey. The system captures the dynamic relationship between the population sizes of predators and prey over time, highlighting the intricate balance between them. In this post we explore this system and calculate its numerical solution using numerical integration Python.
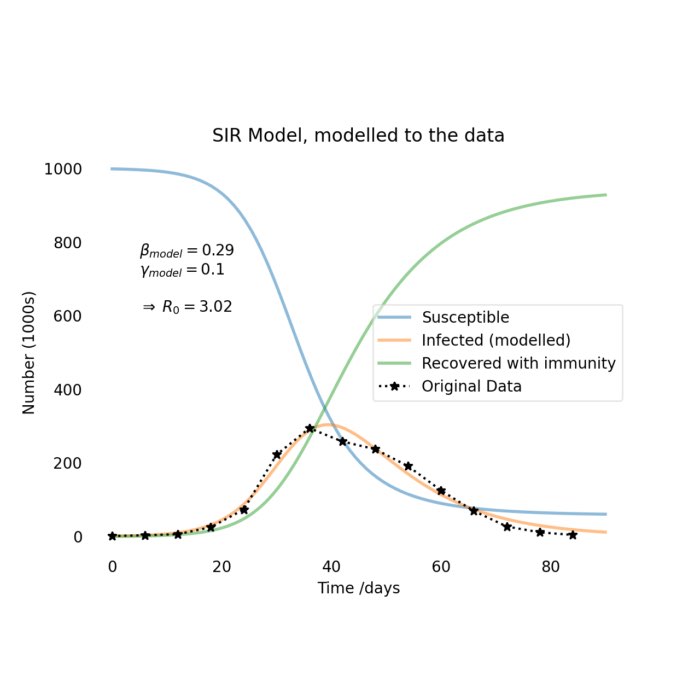
The SIR model: A mathematical approach to epidemic dynamics
In the wake of the COVID-19 pandemic, epidemiological models have garnered significant attention for their ability to provide insights into the spread and control of infectious diseases. One such model is the SIR model, forming the foundation for studying the dynamics of epidemics. In this blog post, we delve into the details of the SIR model, providing a mathematical description, and showcasing its application through a Python simulation.
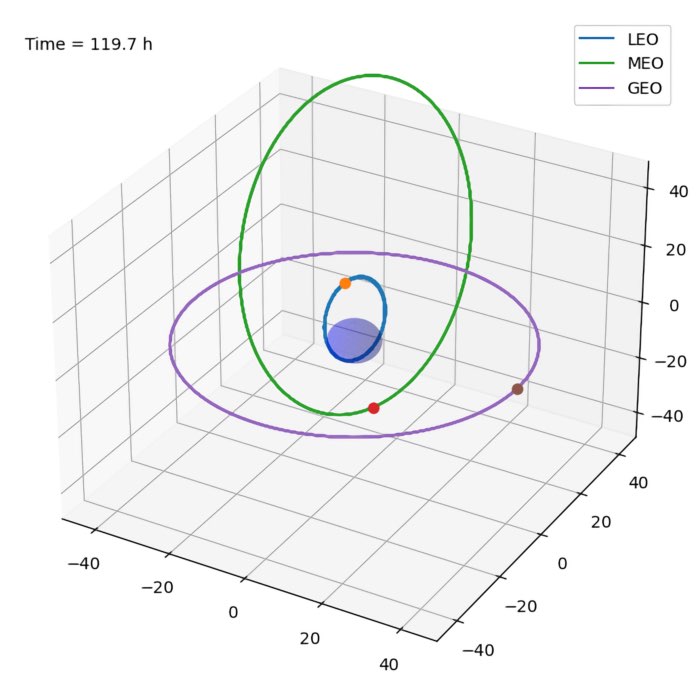
The two-body problem
The two-body system is a classical problem in physics. It describes the motion of two massive objects that are influenced by their mutual gravitational attraction. The two-body problem is a special case of the n-body problem, which describes the motion of two objects that are influenced by their mutual gravitational attraction. In this post, we make use of Runge-Kutta methods to solve the according equations of motion and simulate the trajectories of artificial satellites around the Earth.
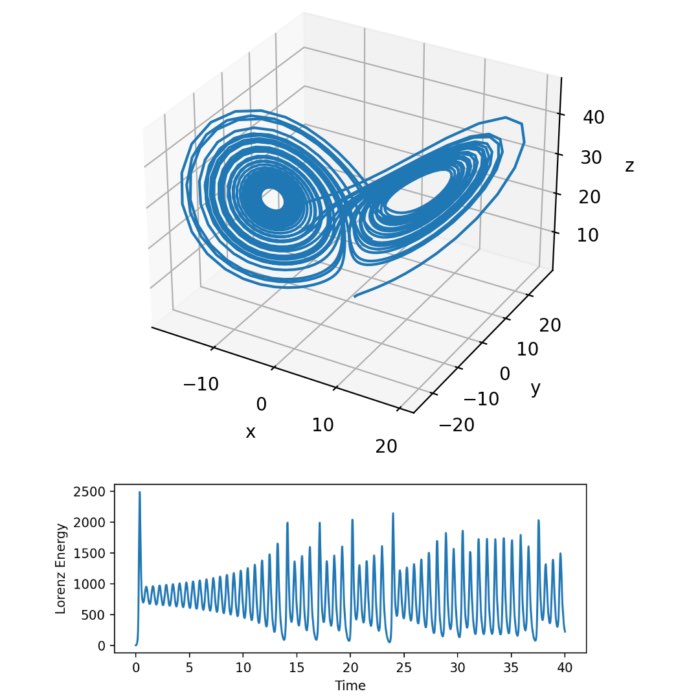
Solving the Lorenz system using Runge-Kutta methods
In my previous post, I introduced the Runge-Kutta methods for numerically solving ordinary differential equations (ODEs), that are challenging to solve analytically. In this post, we apply the Runge-Kutta methods to solve the Lorenz system. The Lorenz system is a set of differential equations known for its chaotic behavior and non-linear dynamics. By utilizing the Runge-Kutta methods, we can effectively simulate and analyze the intricate dynamics of this system.
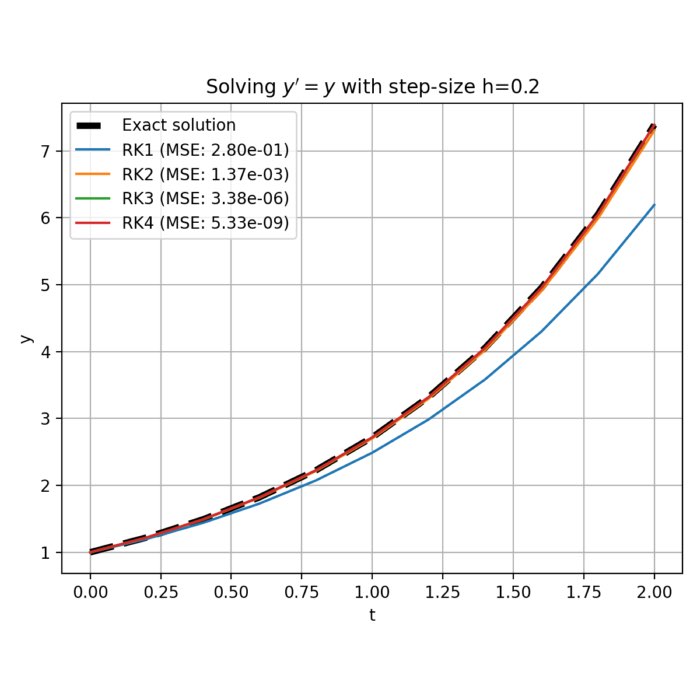
Runge-Kutta methods for solving ODEs
In physics and computational mathematics, numerical methods for solving ordinary differential equations (ODEs) are of central importance. Among these, the family of Runge-Kutta methods stands out due to its versatility and robustness. In this post we compare the first four orders of the Runge-Kutta methods, namely RK1 (Euler’s method), RK2, RK3, and RK4.
Earth's dipolar magnetic field
In physics and computational mathematics, numerical methods for solving ordinary differential equations (ODEs) are of central importance. Among these, the family of Runge-Kutta methods stands out due to its versatility and robustness. In this post we compare the first four orders of the Runge-Kutta methods, namely RK1 (Euler’s method), RK2, RK3, and RK4.
#Data Science (67)
Distinguishing correlation from the coefficient of determination: Proper reporting of r and R²
I noticed that people sometimes report R² (‘R-squared’) instead of the Pearson correlation coefficient r when discussing the correlation between two variables. In the special case of a simple linear relationship this numerical equality is not strictly wrong, yet presenting R² as if it were the correlation coefficient might wrongly give the impression they are the same thing. In this post, we will therefore unpack the difference between these two measures, explain their mathematical definitions and proper usage discuss the best practices for when to use each in statistical reporting.
New teaching material: Functional imaging data analysis – From calcium imaging to network dynamics
We have just completed our new course, Functional Imaging Data Analysis: From Calcium Imaging to Network Dynamics, for the first time as part of the Master of Neuroscience program. This course is now available freely online under ‘Teaching’, alongside my other open educational materials. All resources were created with a strict focus on open content and reproducibility, so that anyone interested can make full use of the lectures, figures, and example code without copyright concerns. Feel free to use and share it.
Miniforge: The minimal, open solution for institutional Python environments
In response to recent licensing changes by Anaconda, Inc., Miniforge has emerged as the recommended minimal installer for Python and scientific computing in academic and research institutions. Now bundling both conda and mamba, Miniforge replaces Miniconda and Mambaforge, ensuring high performance and broad package access via the conda-forge ecosystem. In this post, we briefly demonstrate how to install and migrate to Miniforge, along with troubleshooting tips for common issues in institutional settings.
New teaching material: Dimensionality reduction in neuroscience
We just completed a new two-day course on Dimensionality Reduction in Neuroscience, and I am pleased to announce that the full teaching material is now freely available under a Creative Commons (CC BY 4.0) license. This course is designed to provide an introductory overview of the application of dimensionality reduction techniques for neuroscientists and data scientists alike, focusing on how to handle the increasingly high-dimensional datasets generated by modern neuroscience research.
PyTorch on Apple Silicon
Already some time ago, PyTorch became fully available for Apple Silicon. It’s no longer necessary to install the nightly builds to run PyTorch on the GPU of your Apple Silicon machine as I described in one of my earlier posts.
Understanding Hebbian learning in Hopfield networks
Hopfield networks, a form of recurrent neural network (RNN), serve as a fundamental model for understanding associative memory and pattern recognition in computational neuroscience. Central to the operation of Hopfield networks is the Hebbian learning rule, an idea encapsulated by the maxim ‘neurons that fire together, wire together’. In this post, we explore the mathematical underpinnings of Hebbian learning within Hopfield networks, emphasizing its role in pattern recognition.
Building a neural network from scratch using NumPy
Ever thought about building you own neural network from scratch by simply using NumPy? In this post, we will do exactly that. We will build, from scratch, a simple feedforward neural network and train it on the MNIST dataset.
Python's version logos
Have you ever noticed that Python has introduced individual version logos starting with version 3.10? I couldn’t find any official announcement, but luckily, the Python community on Mastodon was able to help out.
Conditional GANs
I was wondering whether it would be possible to let GANs generate samples conditioned on a specific input type. I wanted the GAN to generate samples of a specific digit, resembling a personal poor man’s mini DALL•E. And indeed, I found a GAN architecture, that allows what I was looking for: Conditional GANs.
Eliminating the middleman: Direct Wasserstein distance computation in WGANs without discriminator
We explore an alternative approach to implementing WGANs. Contrasting from the standard implementation that requires both a generator and discriminator, the method discussed here employs the optimal transport to compute the Wasserstein distance directly between the real and generated data distributions, eliminating the need for a discriminator.
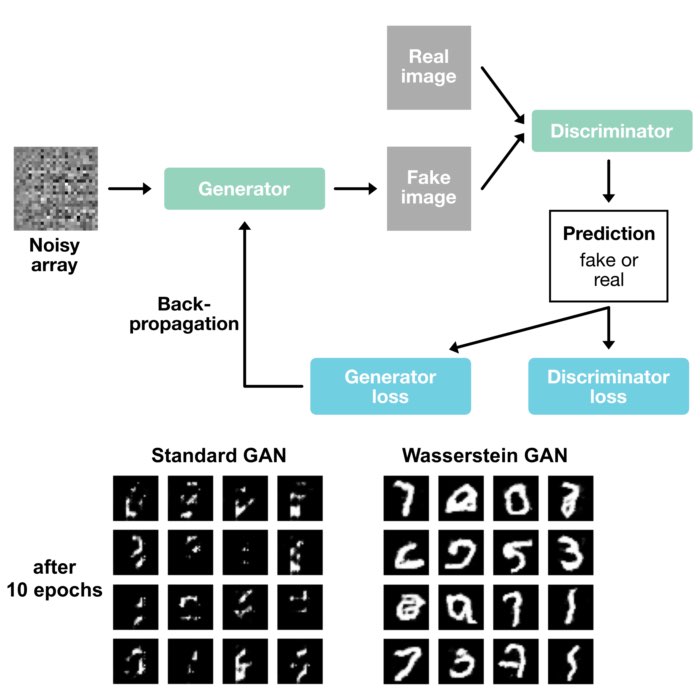
Wasserstein GANs
We apply the Wasserstein distance to Generative Adversarial Networks (GANs) to train them more effectively. We compare a default GAN with a Wasserstein GAN (WGAN) trained on the MNIST dataset and discuss the advantages and disadvantages of both approaches.
Probability distance metrics in machine learning
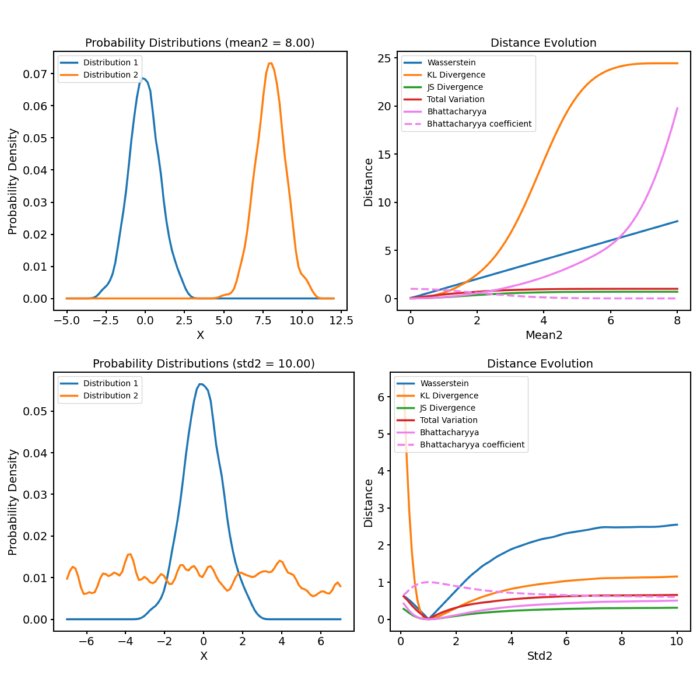
Probabilistic distance metrics play a crucial role in a broad range of machine learning tasks, including clustering, classification, and information retrieval. The choice of metric is often determined by the specific requirements of the task at hand, with each having unique strengths and characteristics. In this post, we discuss five commonly used metrics: the Wasserstein Distance, the Kullback-Leibler Divergence (KL Divergence), the Jensen-Shannon Divergence (JS Divergence), the Total Variation Distance (TV Distance), and the Bhattacharyya Distance.
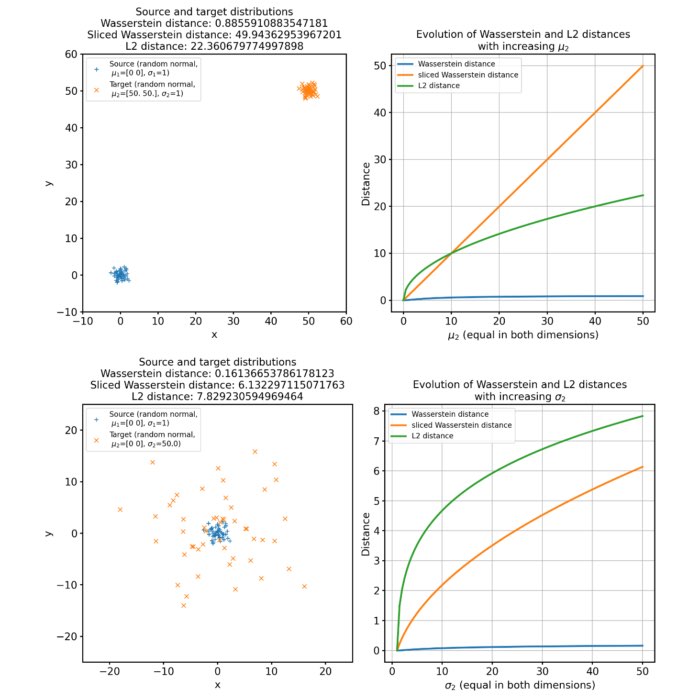
Comparing Wasserstein distance, sliced Wasserstein distance, and L2 norm
In machine learning, especially when dealing with probability distributions or deep generative models, different metrics are used to quantify the ‘distance’ between two distributions. Among these, the Wasserstein distance (EMD), sliced Wasserstein distance (SWD), and the L2 norm, play an important role. Here, we compare these metrics and discuss their advantages and disadvantages.
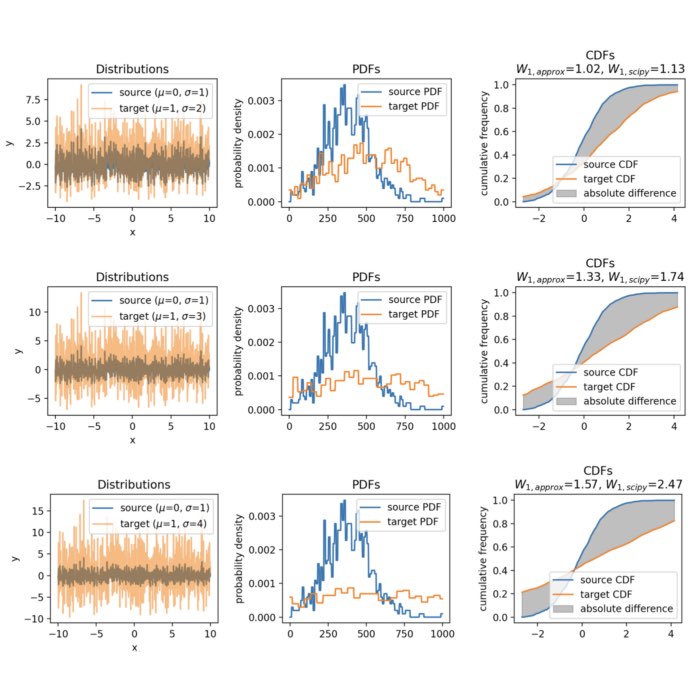
Approximating the Wasserstein distance with cumulative distribution functions
In the previous two posts, we’ve discussed the mathematical details of the Wasserstein distance, exploring its formal definition, its computation through linear programming and the Sinkhorn algorithm. In this post, we take a different approach by approximating the Wasserstein distance with cumulative distribution functions (CDF), providing a more intuitive understanding of the metric.
Wasserstein distance via entropy regularization (Sinkhorn algorithm)
Calculating the Wasserstein distance can be computational costly when using linear programming. The Sinkhorn algorithm provides a computationally efficient method for approximating the Wasserstein distance, making it a practical choice for many applications, especially for large datasets.
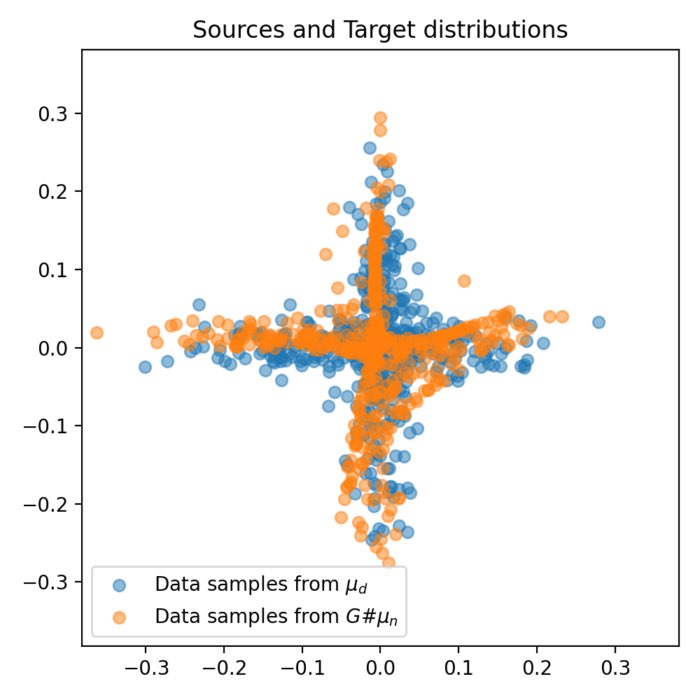
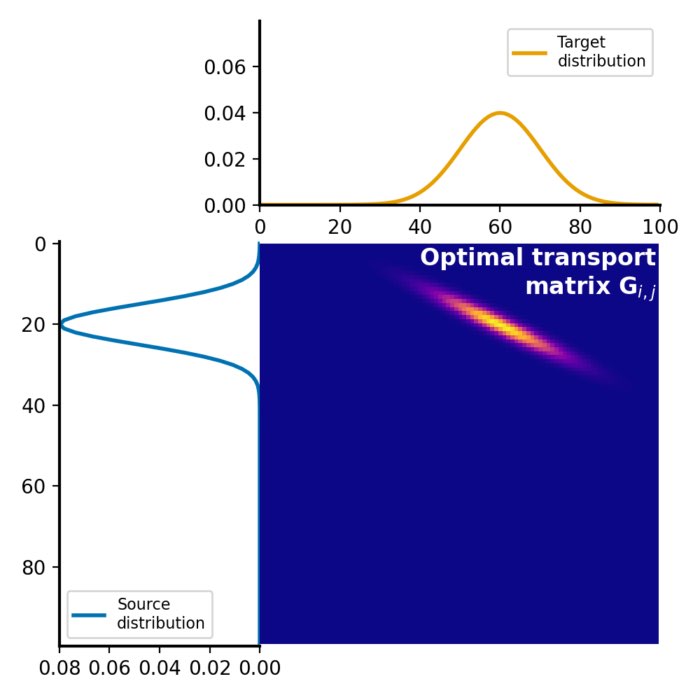
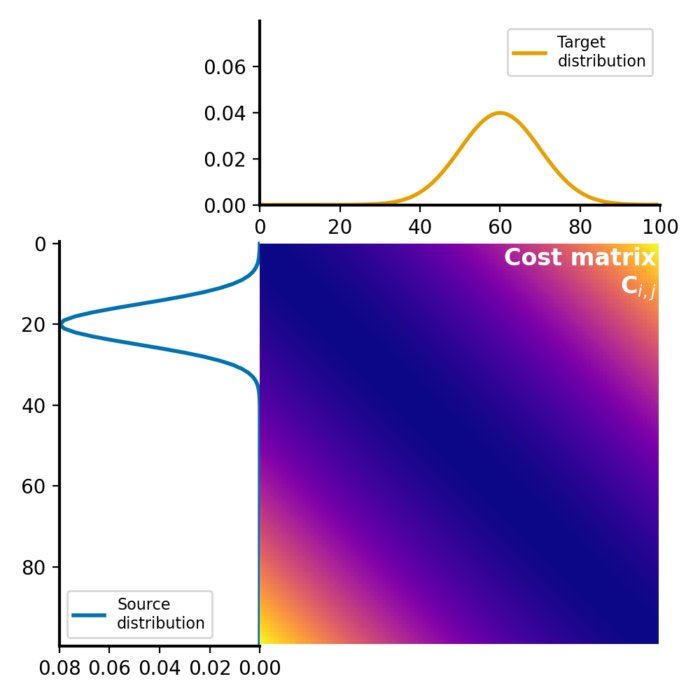
Wasserstein distance and optimal transport
The Wasserstein distance, also known as the Earth Mover’s Distance (EMD), provides a robust and insightful approach for comparing probability distributions and finds application in various fields such as machine learning, data science, image processing, and information theory. In this post, we take a look at the optimal transport problem, required to calculate the Wasserstein distance, and how to calculate the distance metric in Python.
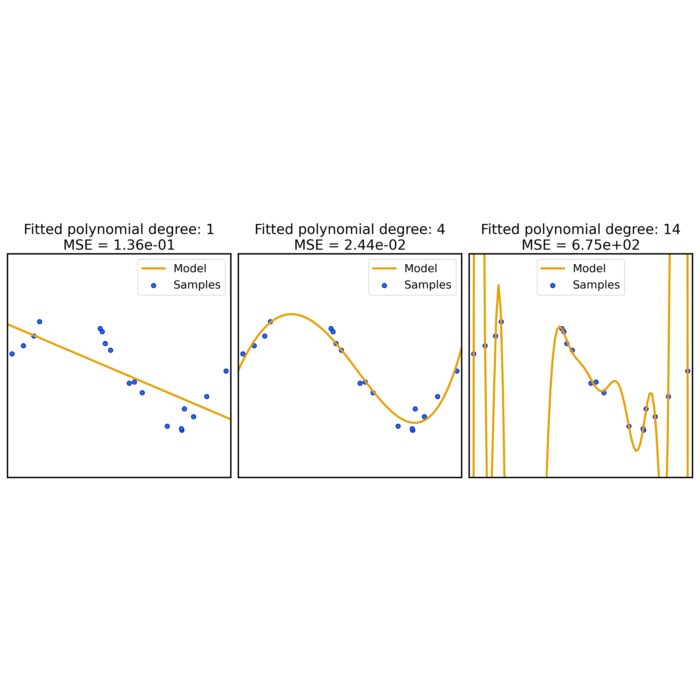
Visualizing Occam's Razor through machine learning
Here, we illustrate the concept of Occam’s Razor, a principle advocating for simplicity, by examining its manifestation in the domain of machine learning using Python.
Mamba vs. Conda: Unleashing lightning-fast Python package installations
If you’ve ever experienced the frustration of waiting for ages while installing Python packages with conda, there’s a game-changer I wish I’d heard about earlier: Mamba. This lightning-fast package manager surprised me with its incredible speed, making package installations a breeze. Here is my personal experience and why Mamba is the speed demon you may have been looking for.
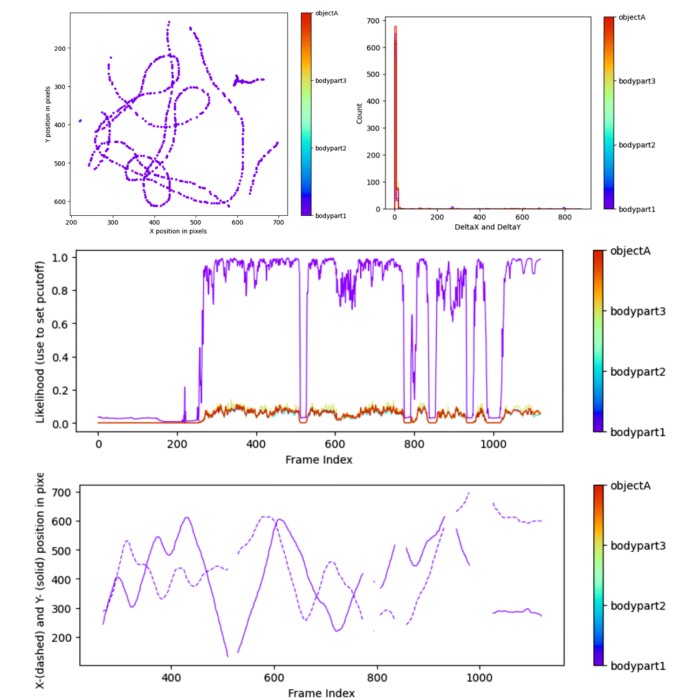
Assessing animal behavior with machine learning: New DeepLabCut tutorial
I have added a hands-on tutorial to the Assessing Animal Behavior lecture. The tutorial covers the GUI-based use of DeepLabCut, a popular open-source software package for markerless pose estimation of animals. The target group is neuroscience students with no or little programming knowledge. Feel free to share the tutorial with students or colleagues who might be interested in using DeepLabCut for their own projects.
Assessing animal behavior with machine learning
High-throughput and multi-modal behavior experiments, coupled with machine learning analysis, unlock valuable insights into complex systems by capturing diverse behavioral responses and deciphering hidden structures within high-dimensional datasets. I just completed a short introductory lecture on this topic, which is now available in the Teachings section.
Bioimage analysis with Napari
I’ve added new teaching material on using the free and open-source software (FOSS) Napari for bioimage analysis. Feel free to use and share it.
Using random forests for pixel classification
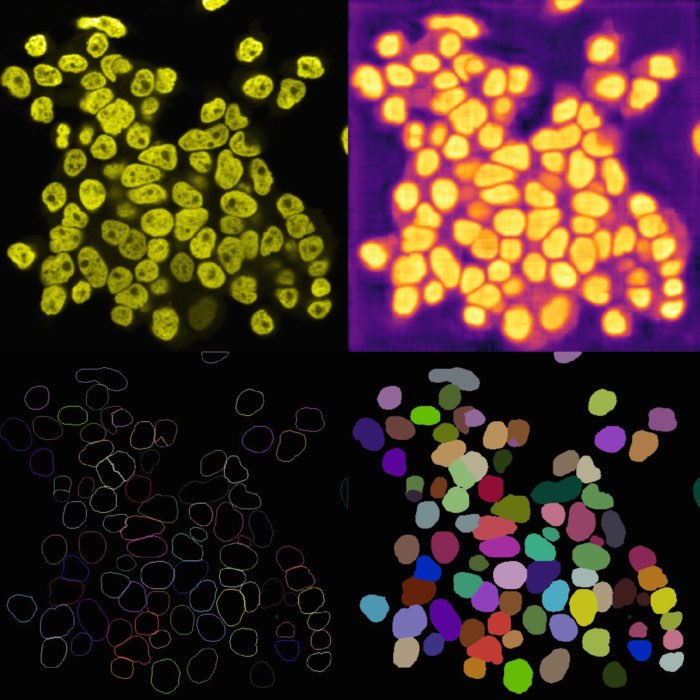
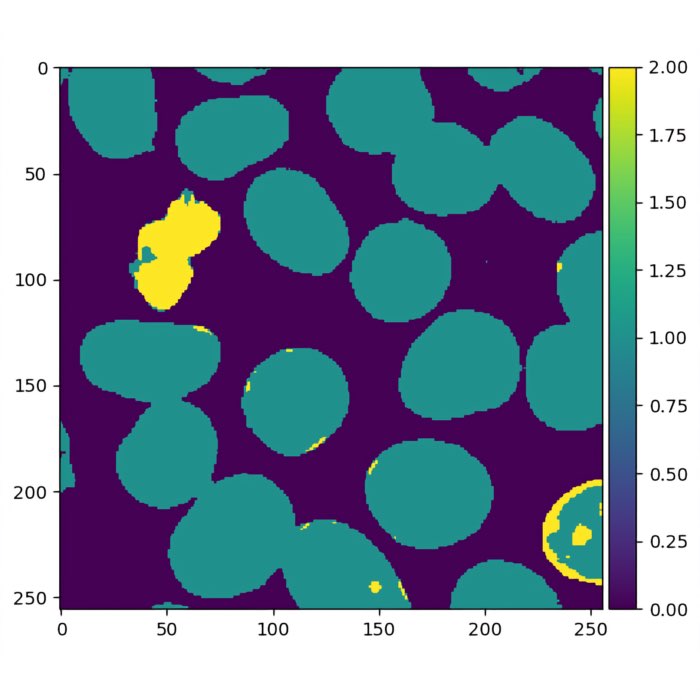
Beyond traditional classification problems, random forests have proven their effectiveness in pixel classification. In this post, we will delve into this domain and explore how random forests can be effectively utilized to tackle the task of pixel classification.
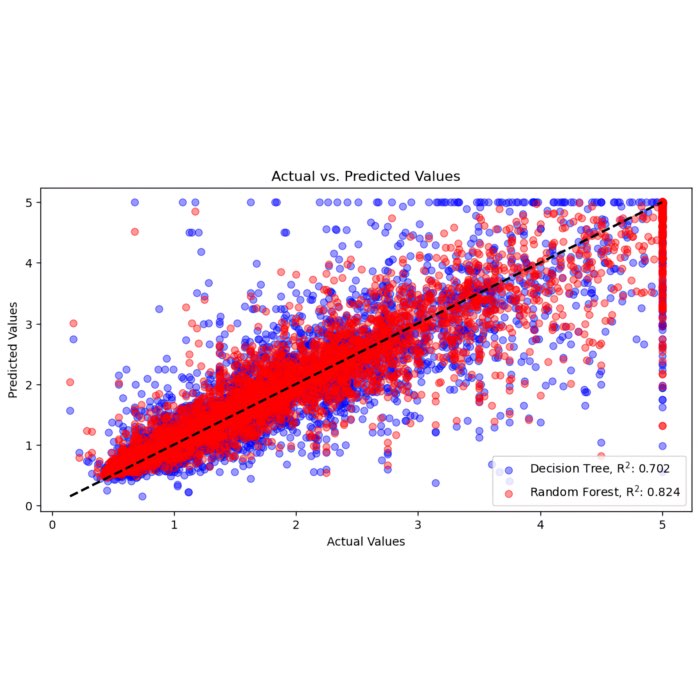
Decision Trees vs. Random Forests for classification and regression: A comparison
Decision trees and random forests are popular machine learning algorithms that are widely used for both classification and regression tasks. In this blog post, we elucidate their theoretical foundations and discuss the differences as well as their advantages and drawbacks.
Image denoising techniques: A comparison of PCA, kernel PCA, autoencoder, and CNN
In this post, we explore the performance of PCA, Kernel PCA, denoising autoencoder, and CNN for image denoising.
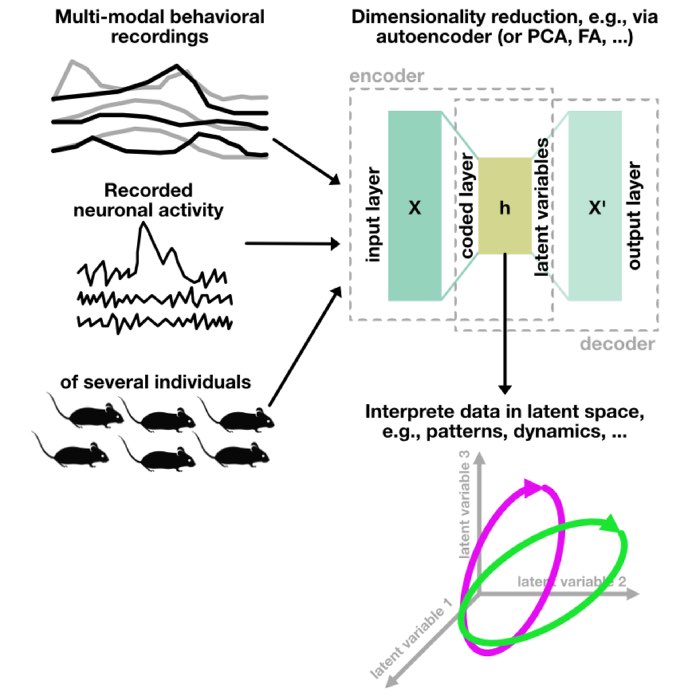
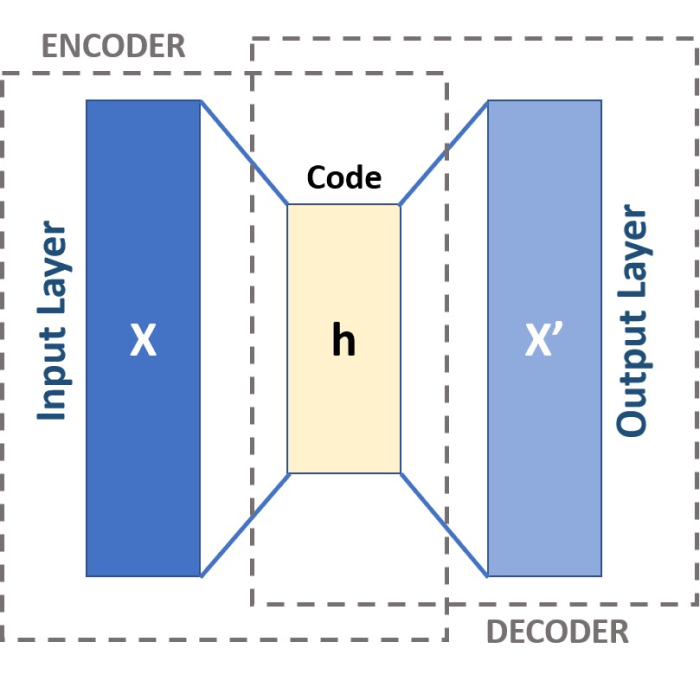
Using Autoencoders to reveal hidden structures in high-dimensional data
In this Python tutorial, we explore the application of Autoencoders for dimensionality reduction, demonstrating how this powerful technique can help us uncover and interpret hidden patterns within our data.
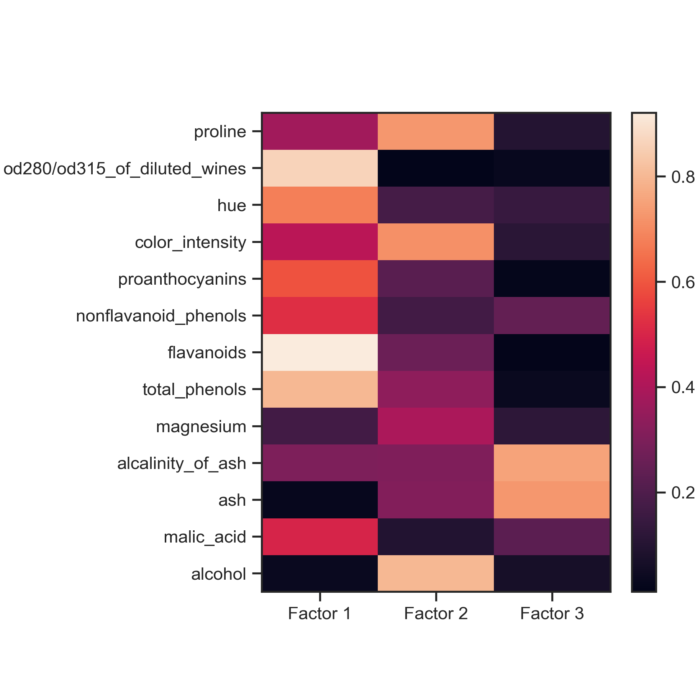
Unlocking hidden patterns with Factor Analysis
In this Python tutorial, we dive into Factor Analysis, a powerful statistical method used to uncover hidden, or ‘latent,’ variables within high-dimensional datasets. Like PCA, grasping this technique will allow us to simplify complex data structures, thereby aiding in more effective data interpretation and decision-making.
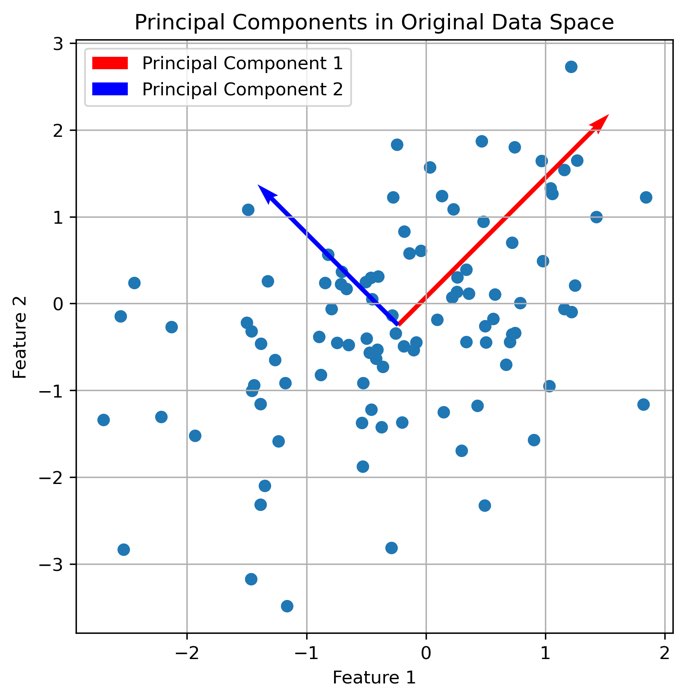
Untangling complexity: harnessing PCA for data dimensionality reduction
This tutorial explores the use of Principal Component Analysis (PCA), a powerful tool for reducing the complexity of high-dimensional data. By delving into both the theoretical underpinnings and practical Python applications, we illuminate how PCA can reveal hidden structures within data and make it more manageable for analysis.
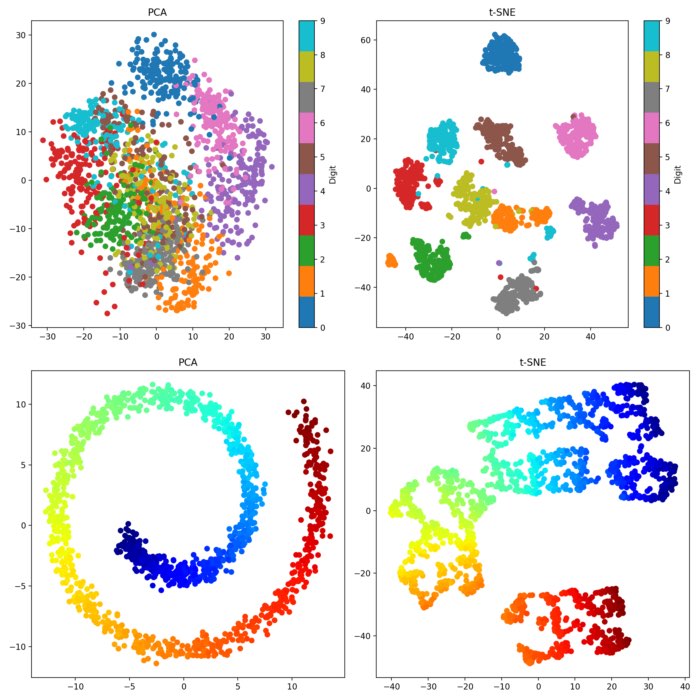
t-SNE and PCA: Two powerful tools for data exploration
Dimensionality reduction techniques play a vital role in both data exploration and visualization. Among these techniques, t-SNE and PCA are widely used and offer valuable insights into complex datasets. In this blog post, we explore te mathematical background of both methods, compare their methodologies, and discuss their advantages and disadvantages. Additionally, we take a look at their practical implementation in Python and compare the results on different sample datasets.
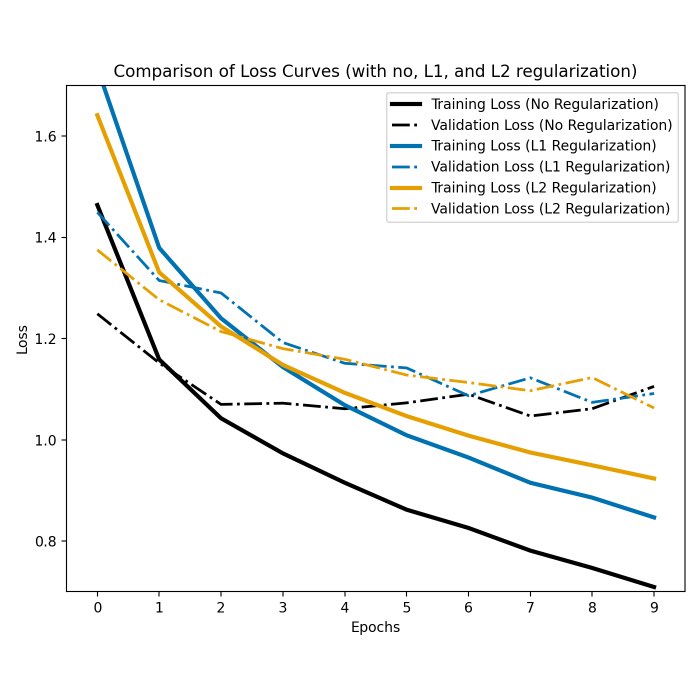
Understanding L1 and L2 regularization in machine learning
Regularization techniques play a vital role in preventing overfitting and enhancing the generalization capability of machine learning models. Among these techniques, L1 and L2 regularization are widely employed for their effectiveness in controlling model complexity. In this blog post, we explore the concepts of L1 and L2 regularization and provide a practical demonstration in Python.
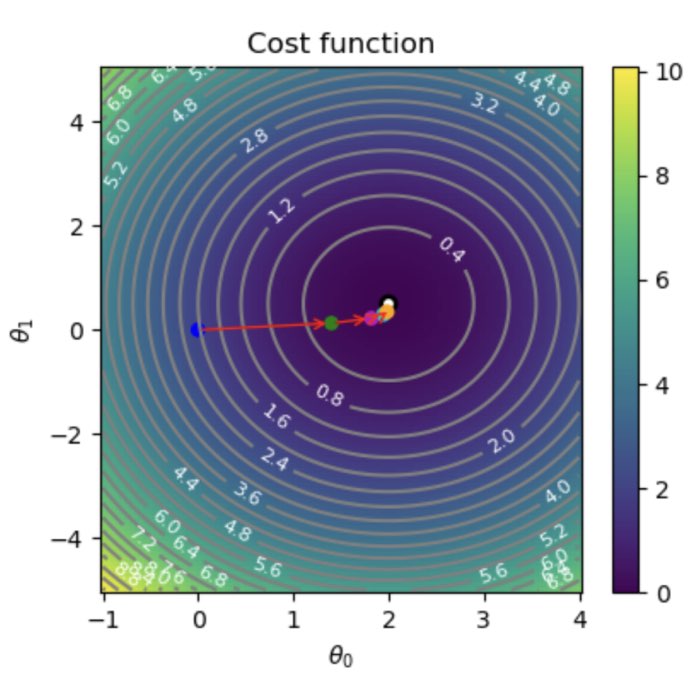
Understanding gradient descent in machine learning
Gradient descent is a fundamental optimization algorithm widely used in machine learning for finding the optimal parameters of a model. It is a powerful technique that enables models to learn from data by iteratively adjusting their parameters to minimize a cost or loss function. In this blog post, we explore the mathematical background of this method and showcase its implementation in Python.
Loading and saving files in Google Colab
Enable I/O support in your notebooks running in Google Colab with just a few additional commands.
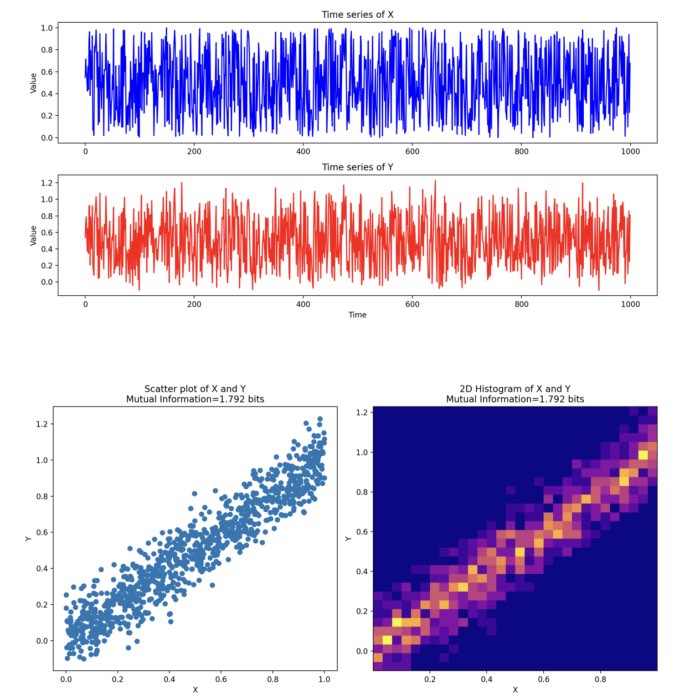
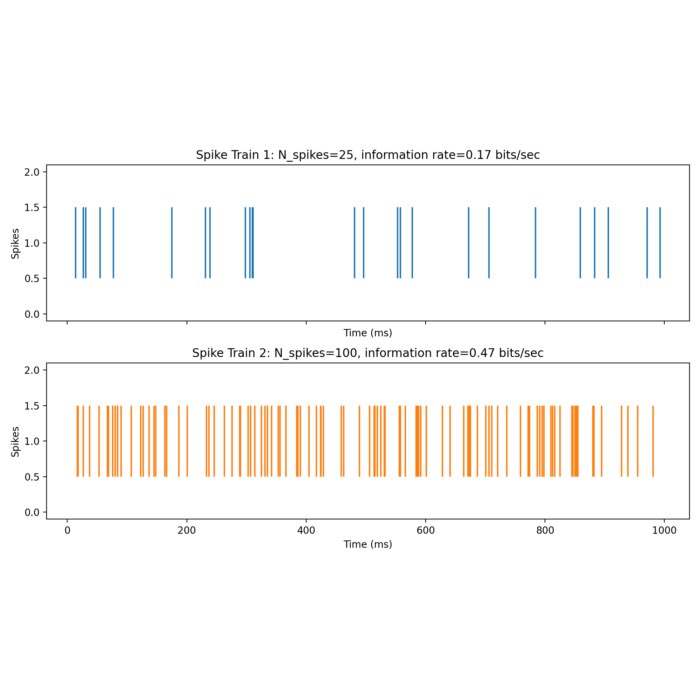
Mutual information and its relationship to information entropy
Mutual information is an essential measure in information theory that quantifies the statistical dependence between two random variables. Given its broad applicability, it has become an invaluable tool in diverse fields like machine learning, neuroscience, signal processing, and more. This post explores the mathematical foundations of mutual information and its relationship to information entropy. We will also demonstrate its implementation in some Python examples.
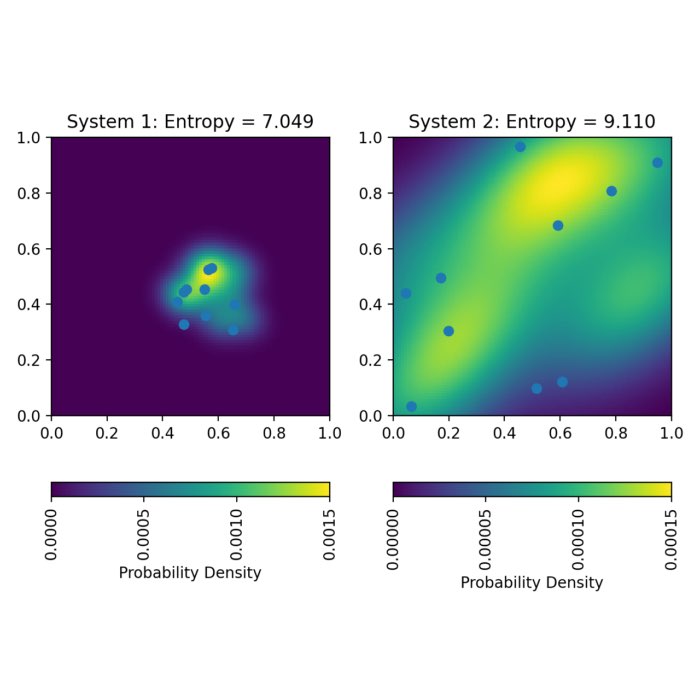
Information entropy
A fundamental concept that plays a pivotal role in quantifying the uncertainty or randomness of a set of data is the information entropy. Information entropy provides a measure of the average amount of information or surprise contained in a random variable. In this blog post, we explore its mathematical foundations and demonstrate its implementation in some Python examples.
Understanding entropy
In physics, entropy is a fundamental concept that plays a crucial role in understanding the behavior of physical systems. It provides a measure of the disorder or randomness within a system, and its study has far-reaching applications across various branches of physics. This blog post aims to provide a brief overview of entropy in order to gain a better understanding of it.
Bio-image registration with Python
Which method works best for which registration problem? In this tutorial we compare different methods for the registration of bio-images using Python.
How to run PyTorch on the M1 Mac GPU
As for TensorFlow, it takes only a few steps to enable a Mac with M1 chip (Apple silicon) for machine learning tasks in Python with PyTorch.
How to run TensorFlow on the M1 Mac GPU
In just a few steps you can enable a Mac with M1 chip (Apple silicon) for machine learning tasks in Python with TensorFlow.
Is there a difference between miniconda and miniforge?
Simply said: not really. Miniconda is the company driven minimal conda installer, while miniforge is its community driven variant. In the end, you’ll get the same minimal conda installation on your machine – with a minor difference.
Hacks and extensions to improve your coding with Visual Studio Code
This curated list contains useful hacks and extensions to improve the overall coding performance with Visual Studio Code (VS Code).
Setting up Visual Studio Code for Python
In just a few steps you can turn Visual Studio Code (VS Code) into a powerful Python editor for both pure Python code and Jupyter Notebooks.
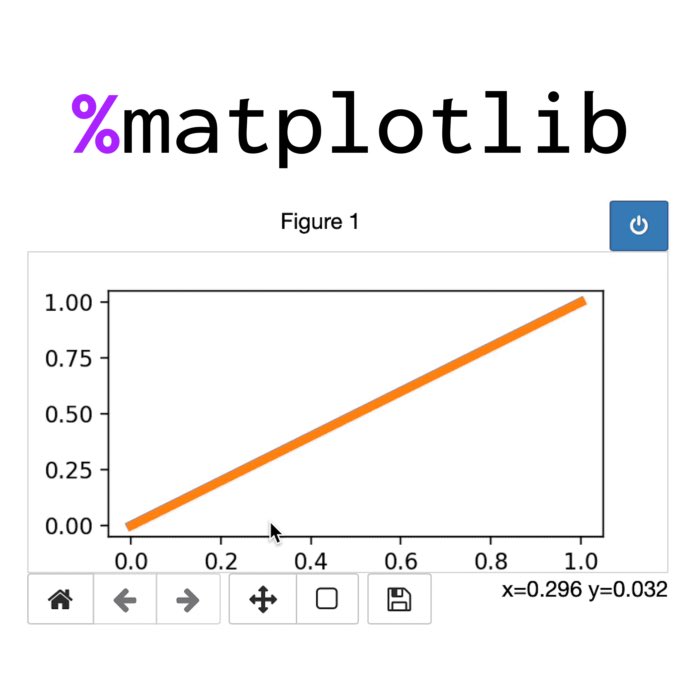
Enable interactive plots and other plot modes in Jupyter notebooks
Learn how to enable interactive, static and stand-alone window plots in Jupyter notebooks with the magic command
%matplotlib.
Enable code folding in JupyterLab
Learn how to enable code folding in JupyterLab for both, Jupyter Notebooks and pure Python scripts.
How to create and apply a requirements.txt file in Python
Learn how to install Python packages with a requirements.txt file and how to create one yourself.
Virtual environments with venv
In addition to conda’s
create command, Python’s built-in venv command offers another way for creating virtual environments.
Using pip to install Python packages
pip is another package installer for Python. Learn how to use it for installing and managing Python packages in your projects.
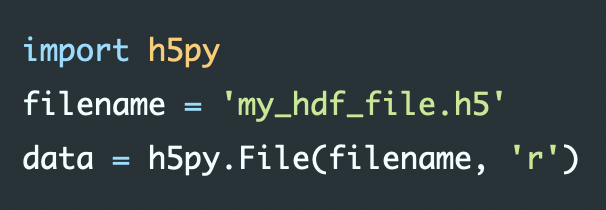
How to install and run Python code from GitHub
Learn how to install code from GitHub, that is, e.g., not (yet) available via conda or pip.
A minimal Python installation with miniconda
Learn how to install miniconda to have a quick and minimal Python installation on any operating system. Also learn how to use conda to create and manage virtual environments, install packages, run Python scripts and run Jupyter Notebooks and JupyterLab.
Stable installation of Napari on a M1 Mac
In case you’re having problems installing Napari on your M1 Mac, try to install it from conda instead of pip.
Using Zarr for images – The OME-ZARR standard
As for any other NumPy array, we can use the Zarr file format to store image files. In this post we additionally explore the NGFF (next-generation file format) OME-ZARR standard.
Zarr – or: How to save NumPy arrays
What is Zarr and why is it probably the most suitable file format for saving NumPy arrays?
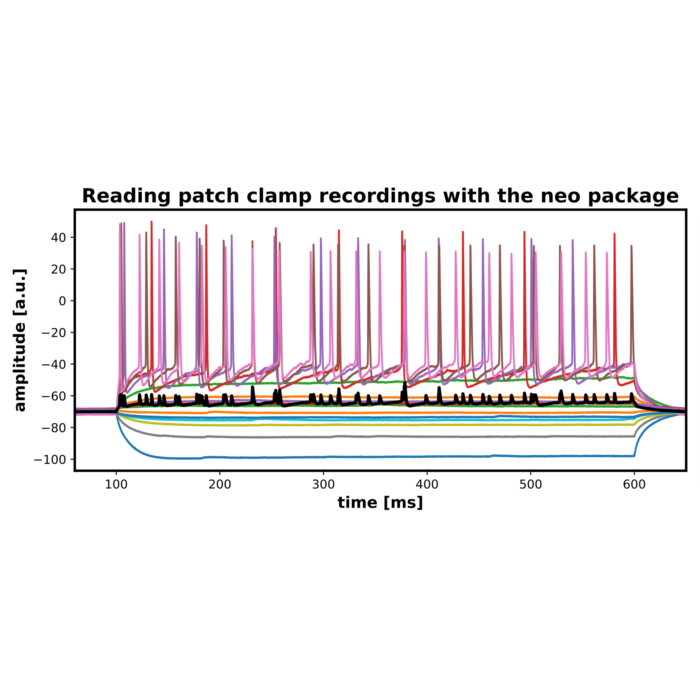
How to read patch clamp recordings in WaveMetrics IGOR binary files (ibw) in Python
This is a mini tutorial on how to read patch clamp recordings in WaveMetrics IGOR binary files (*.ibw) in Python using the neo and igor packages.
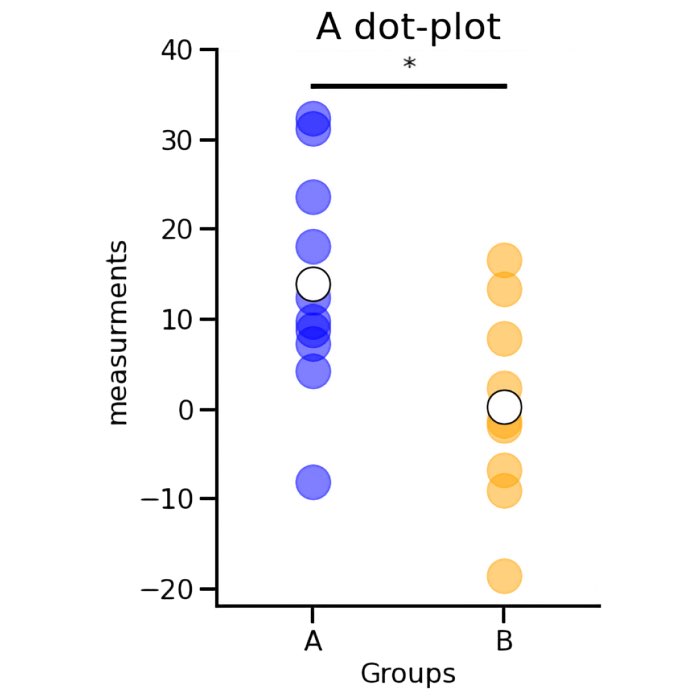
How to add statistical annotations to matplotlib plots
This mini tutorial shows, how to add statistical annotations to matplotlib plots with just a few commands.
Variable Explorer in Jupyter Notebooks
Extend your Jupyter environment with Notebook Extensions and enable, e.g., the option to explore your currently defined variables in a running Jupyter session.
Opening a Jupyter notebook from GitHub in Binder: A step-by-step guide
Opening a Jupyter notebook from GitHub in Binder simplifies access to shared code and facilitates seamless collaboration. With just a few steps, you can launch and interact with Jupyter notebooks directly in your browser, without the need for complex setup procedures.
New Teaching Material: Python Cheat Sheets
I’ve started a collection of various Python cheat sheets that contain some useful and commonly used commands and usage examples.
New Teaching Material: Statistical data analysis and basic time series analysis with Python
I’ve added two new tutorials in the teaching section on statistical data analysis and basic time series analysis with Python.
New Teaching Material: Analyzing IGOR binary files of patch clamp recordings
I’ve added a new tutorial in the teaching section on how to read and process IGOR binary files (ibw) of patch clamp recordings.
The Weierstrass function and the beauty of fractals
Fractals are captivating mathematical objects that exhibit intricate patterns and self-similarity at various scales. In this post, we explore the elegance and significance of the Weierstrass function, its relation to fractals and fractal geometry, and discuss other notable fractals. Through this journey, we will discover the fascinating world of fractal geometry and its beautiful and profound impact.
The Lotka-Volterra equations: Modeling predator-prey dynamics
The Lotka-Volterra system, also known as the predator-prey equations, is a mathematical model that describes the interaction between two species: predators and their prey. The system captures the dynamic relationship between the population sizes of predators and prey over time, highlighting the intricate balance between them. In this post we explore this system and calculate its numerical solution using numerical integration Python.
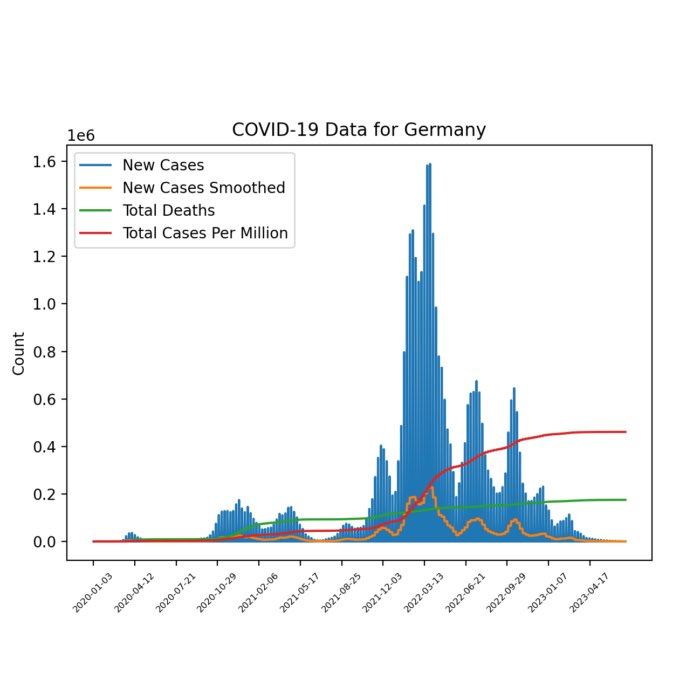
Interactive COVID-19 data exploration with Jupyter notebooks
Amidst the ongoing challenges of the COVID-19 pandemic, I have written a Jupyter notebook that facilitates interactive exploration of COVID-19 data. You can select specific countries and visualize key aspects such as confirmed cases, deaths, and vaccinations. The notebook is openly available on GitHub. Feel free to use and share it.
The SIR model: A mathematical approach to epidemic dynamics
In the wake of the COVID-19 pandemic, epidemiological models have garnered significant attention for their ability to provide insights into the spread and control of infectious diseases. One such model is the SIR model, forming the foundation for studying the dynamics of epidemics. In this blog post, we delve into the details of the SIR model, providing a mathematical description, and showcasing its application through a Python simulation.
The two-body problem
The two-body system is a classical problem in physics. It describes the motion of two massive objects that are influenced by their mutual gravitational attraction. The two-body problem is a special case of the n-body problem, which describes the motion of two objects that are influenced by their mutual gravitational attraction. In this post, we make use of Runge-Kutta methods to solve the according equations of motion and simulate the trajectories of artificial satellites around the Earth.
Solving the Lorenz system using Runge-Kutta methods
In my previous post, I introduced the Runge-Kutta methods for numerically solving ordinary differential equations (ODEs), that are challenging to solve analytically. In this post, we apply the Runge-Kutta methods to solve the Lorenz system. The Lorenz system is a set of differential equations known for its chaotic behavior and non-linear dynamics. By utilizing the Runge-Kutta methods, we can effectively simulate and analyze the intricate dynamics of this system.
Runge-Kutta methods for solving ODEs
In physics and computational mathematics, numerical methods for solving ordinary differential equations (ODEs) are of central importance. Among these, the family of Runge-Kutta methods stands out due to its versatility and robustness. In this post we compare the first four orders of the Runge-Kutta methods, namely RK1 (Euler’s method), RK2, RK3, and RK4.
Earth's dipolar magnetic field
In physics and computational mathematics, numerical methods for solving ordinary differential equations (ODEs) are of central importance. Among these, the family of Runge-Kutta methods stands out due to its versatility and robustness. In this post we compare the first four orders of the Runge-Kutta methods, namely RK1 (Euler’s method), RK2, RK3, and RK4.
#Image Processing (9)
New teaching material: Functional imaging data analysis – From calcium imaging to network dynamics
We have just completed our new course, Functional Imaging Data Analysis: From Calcium Imaging to Network Dynamics, for the first time as part of the Master of Neuroscience program. This course is now available freely online under ‘Teaching’, alongside my other open educational materials. All resources were created with a strict focus on open content and reproducibility, so that anyone interested can make full use of the lectures, figures, and example code without copyright concerns. Feel free to use and share it.
Bioimage analysis with Napari
I’ve added new teaching material on using the free and open-source software (FOSS) Napari for bioimage analysis. Feel free to use and share it.
Image denoising techniques: A comparison of PCA, kernel PCA, autoencoder, and CNN
In this post, we explore the performance of PCA, Kernel PCA, denoising autoencoder, and CNN for image denoising.
Bio-image registration with Python
Which method works best for which registration problem? In this tutorial we compare different methods for the registration of bio-images using Python.
Stable installation of Napari on a M1 Mac
In case you’re having problems installing Napari on your M1 Mac, try to install it from conda instead of pip.
Using Zarr for images – The OME-ZARR standard
As for any other NumPy array, we can use the Zarr file format to store image files. In this post we additionally explore the NGFF (next-generation file format) OME-ZARR standard.
Zarr – or: How to save NumPy arrays
What is Zarr and why is it probably the most suitable file format for saving NumPy arrays?
New Teaching Material: Fiji short course
There is a new tutorial in the Teaching Material. It’s a short Fiji tutorial on analyzing biomedical image data.
#Independent Web (11)
Reflections on joining Bluesky: Opportunities and risks for the scientific community
Over the past two weeks, I have taken a closer look at Bluesky, exploring its features and dynamics through the lens of my own experience within the neuroscience community. So far, my impressions have been mixed: while some aspects of Bluesky are genuinely promising, others evoke certain concerns about the future of scientific communities on digital platforms. In this post, I would like to share a personal reflection on this recent shift, situating it within the broader context of academic social media migration.
How to get an RSS feed of your Mastodon bookmarks
The third-party service Mastodon Bookmark RSS allows you to subscribe to your Mastodon bookmarks via RSS, so you don’t forget to make use out of them. You can even integrate the feed into your favorite Zettelkasten apps such as DEVONthink and Obsidian.
Moving a Mastodon account to another server
I recently moved my Mastodon account to a new server, including all my followers. I was surprised, how easy and seamless it worked. Here is a how-to, summarizing the migration steps.
I'm on Mastodon
Mastodon is not just a Twitter alternative. It’s a free and open-source social media platform of its own kind. Here is my story how I got there.
On website subscriptions via RSS and Atom feeds
Personal opinion on how to create and maintain personal news feeds beyond the dependence on big social media and tech companies.
Dealing with future posts in Jekyll
While drafting blog posts in Jekyll, you may want to keep some posts hidden from the public eye until they’re ready to be published. In the world of blogging with Jekyll, there are several effective methods to draft such posts without immediately publishing them. Here are three practical approaches.
Running and testing your Jekyll site locally with custom options
Developing with Jekyll often requires running your site locally to test changes before deploying them live. Here is a handy yet useful one-line command that I usually use to run my Jekyll site locally with custom options.
Running a personal website with Jekyll
I have redesigned my website and moved it to a new host as well: I’m running it as personal Jekyll website hosted on GitHub now.
#Jekyll (13)
On website subscriptions via RSS and Atom feeds
Personal opinion on how to create and maintain personal news feeds beyond the dependence on big social media and tech companies.
Dealing with future posts in Jekyll
While drafting blog posts in Jekyll, you may want to keep some posts hidden from the public eye until they’re ready to be published. In the world of blogging with Jekyll, there are several effective methods to draft such posts without immediately publishing them. Here are three practical approaches.
Running and testing your Jekyll site locally with custom options
Developing with Jekyll often requires running your site locally to test changes before deploying them live. Here is a handy yet useful one-line command that I usually use to run my Jekyll site locally with custom options.
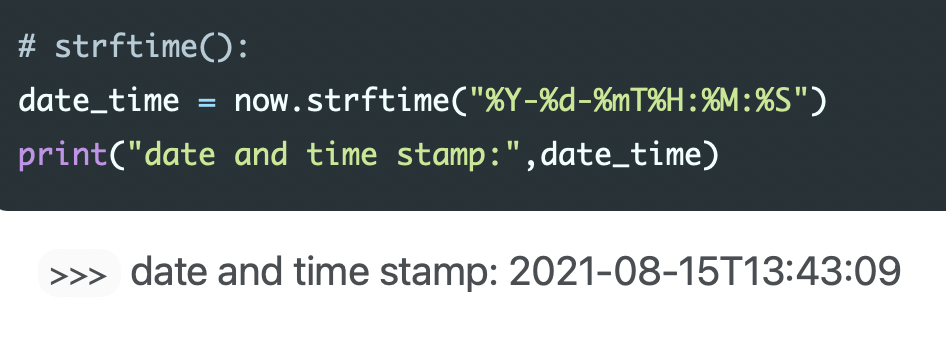
strftime Cheat Sheet
Cheat Sheet on formatted date and time strings used, e.g., in Python, C/C++ or even on Jekyll websites by using Liquid tags.
Liquid Cheat Sheet
This Cheat Sheet gives an overview of Liquid syntax commands one might encounter while developing a Jekyll website.
Minimal Mistakes Cheat Sheet
A quick overview of available commands for creating content with the Minimal Mistakes Jekyll theme.
New Teaching Material: LaTeX Guide
I’ve added a LaTeX guide to the General Teaching Materials in the teaching section. It serves as a Getting started with LaTeX guide and as a LaTeX glossary.
Running a personal website with Jekyll
I have redesigned my website and moved it to a new host as well: I’m running it as personal Jekyll website hosted on GitHub now.
#Machine Learning/AI (28)
New teaching material: Functional imaging data analysis – From calcium imaging to network dynamics
We have just completed our new course, Functional Imaging Data Analysis: From Calcium Imaging to Network Dynamics, for the first time as part of the Master of Neuroscience program. This course is now available freely online under ‘Teaching’, alongside my other open educational materials. All resources were created with a strict focus on open content and reproducibility, so that anyone interested can make full use of the lectures, figures, and example code without copyright concerns. Feel free to use and share it.
PyTorch on Apple Silicon
Already some time ago, PyTorch became fully available for Apple Silicon. It’s no longer necessary to install the nightly builds to run PyTorch on the GPU of your Apple Silicon machine as I described in one of my earlier posts.
Understanding Hebbian learning in Hopfield networks
Hopfield networks, a form of recurrent neural network (RNN), serve as a fundamental model for understanding associative memory and pattern recognition in computational neuroscience. Central to the operation of Hopfield networks is the Hebbian learning rule, an idea encapsulated by the maxim ‘neurons that fire together, wire together’. In this post, we explore the mathematical underpinnings of Hebbian learning within Hopfield networks, emphasizing its role in pattern recognition.
Building a neural network from scratch using NumPy
Ever thought about building you own neural network from scratch by simply using NumPy? In this post, we will do exactly that. We will build, from scratch, a simple feedforward neural network and train it on the MNIST dataset.
Conditional GANs
I was wondering whether it would be possible to let GANs generate samples conditioned on a specific input type. I wanted the GAN to generate samples of a specific digit, resembling a personal poor man’s mini DALL•E. And indeed, I found a GAN architecture, that allows what I was looking for: Conditional GANs.
Eliminating the middleman: Direct Wasserstein distance computation in WGANs without discriminator
We explore an alternative approach to implementing WGANs. Contrasting from the standard implementation that requires both a generator and discriminator, the method discussed here employs the optimal transport to compute the Wasserstein distance directly between the real and generated data distributions, eliminating the need for a discriminator.
Wasserstein GANs
We apply the Wasserstein distance to Generative Adversarial Networks (GANs) to train them more effectively. We compare a default GAN with a Wasserstein GAN (WGAN) trained on the MNIST dataset and discuss the advantages and disadvantages of both approaches.
Probability distance metrics in machine learning
Probabilistic distance metrics play a crucial role in a broad range of machine learning tasks, including clustering, classification, and information retrieval. The choice of metric is often determined by the specific requirements of the task at hand, with each having unique strengths and characteristics. In this post, we discuss five commonly used metrics: the Wasserstein Distance, the Kullback-Leibler Divergence (KL Divergence), the Jensen-Shannon Divergence (JS Divergence), the Total Variation Distance (TV Distance), and the Bhattacharyya Distance.
Comparing Wasserstein distance, sliced Wasserstein distance, and L2 norm
In machine learning, especially when dealing with probability distributions or deep generative models, different metrics are used to quantify the ‘distance’ between two distributions. Among these, the Wasserstein distance (EMD), sliced Wasserstein distance (SWD), and the L2 norm, play an important role. Here, we compare these metrics and discuss their advantages and disadvantages.
Approximating the Wasserstein distance with cumulative distribution functions
In the previous two posts, we’ve discussed the mathematical details of the Wasserstein distance, exploring its formal definition, its computation through linear programming and the Sinkhorn algorithm. In this post, we take a different approach by approximating the Wasserstein distance with cumulative distribution functions (CDF), providing a more intuitive understanding of the metric.
Wasserstein distance via entropy regularization (Sinkhorn algorithm)
Calculating the Wasserstein distance can be computational costly when using linear programming. The Sinkhorn algorithm provides a computationally efficient method for approximating the Wasserstein distance, making it a practical choice for many applications, especially for large datasets.
Wasserstein distance and optimal transport
The Wasserstein distance, also known as the Earth Mover’s Distance (EMD), provides a robust and insightful approach for comparing probability distributions and finds application in various fields such as machine learning, data science, image processing, and information theory. In this post, we take a look at the optimal transport problem, required to calculate the Wasserstein distance, and how to calculate the distance metric in Python.
Visualizing Occam's Razor through machine learning
Here, we illustrate the concept of Occam’s Razor, a principle advocating for simplicity, by examining its manifestation in the domain of machine learning using Python.
Integrate and Fire Model: A simple neuronal model
In this post we explore the Integrate-and-Fire model, a simplified representation of a neuron. We also run some simulations in Python to understand the model dynamics.
Assessing animal behavior with machine learning: New DeepLabCut tutorial
I have added a hands-on tutorial to the Assessing Animal Behavior lecture. The tutorial covers the GUI-based use of DeepLabCut, a popular open-source software package for markerless pose estimation of animals. The target group is neuroscience students with no or little programming knowledge. Feel free to share the tutorial with students or colleagues who might be interested in using DeepLabCut for their own projects.
Assessing animal behavior with machine learning
High-throughput and multi-modal behavior experiments, coupled with machine learning analysis, unlock valuable insights into complex systems by capturing diverse behavioral responses and deciphering hidden structures within high-dimensional datasets. I just completed a short introductory lecture on this topic, which is now available in the Teachings section.
Bioimage analysis with Napari
I’ve added new teaching material on using the free and open-source software (FOSS) Napari for bioimage analysis. Feel free to use and share it.
Using random forests for pixel classification
Beyond traditional classification problems, random forests have proven their effectiveness in pixel classification. In this post, we will delve into this domain and explore how random forests can be effectively utilized to tackle the task of pixel classification.
Decision Trees vs. Random Forests for classification and regression: A comparison
Decision trees and random forests are popular machine learning algorithms that are widely used for both classification and regression tasks. In this blog post, we elucidate their theoretical foundations and discuss the differences as well as their advantages and drawbacks.
Image denoising techniques: A comparison of PCA, kernel PCA, autoencoder, and CNN
In this post, we explore the performance of PCA, Kernel PCA, denoising autoencoder, and CNN for image denoising.
Using Autoencoders to reveal hidden structures in high-dimensional data
In this Python tutorial, we explore the application of Autoencoders for dimensionality reduction, demonstrating how this powerful technique can help us uncover and interpret hidden patterns within our data.
Unlocking hidden patterns with Factor Analysis
In this Python tutorial, we dive into Factor Analysis, a powerful statistical method used to uncover hidden, or ‘latent,’ variables within high-dimensional datasets. Like PCA, grasping this technique will allow us to simplify complex data structures, thereby aiding in more effective data interpretation and decision-making.
Untangling complexity: harnessing PCA for data dimensionality reduction
This tutorial explores the use of Principal Component Analysis (PCA), a powerful tool for reducing the complexity of high-dimensional data. By delving into both the theoretical underpinnings and practical Python applications, we illuminate how PCA can reveal hidden structures within data and make it more manageable for analysis.
t-SNE and PCA: Two powerful tools for data exploration
Dimensionality reduction techniques play a vital role in both data exploration and visualization. Among these techniques, t-SNE and PCA are widely used and offer valuable insights into complex datasets. In this blog post, we explore te mathematical background of both methods, compare their methodologies, and discuss their advantages and disadvantages. Additionally, we take a look at their practical implementation in Python and compare the results on different sample datasets.
Understanding L1 and L2 regularization in machine learning
Regularization techniques play a vital role in preventing overfitting and enhancing the generalization capability of machine learning models. Among these techniques, L1 and L2 regularization are widely employed for their effectiveness in controlling model complexity. In this blog post, we explore the concepts of L1 and L2 regularization and provide a practical demonstration in Python.
Understanding gradient descent in machine learning
Gradient descent is a fundamental optimization algorithm widely used in machine learning for finding the optimal parameters of a model. It is a powerful technique that enables models to learn from data by iteratively adjusting their parameters to minimize a cost or loss function. In this blog post, we explore the mathematical background of this method and showcase its implementation in Python.
How to run PyTorch on the M1 Mac GPU
As for TensorFlow, it takes only a few steps to enable a Mac with M1 chip (Apple silicon) for machine learning tasks in Python with PyTorch.
How to run TensorFlow on the M1 Mac GPU
In just a few steps you can enable a Mac with M1 chip (Apple silicon) for machine learning tasks in Python with TensorFlow.
#Markdown/LaTeX (30)
Bridging ideas on the go: WikiLinks come to DEVONthink To Go
The WikiLinks feature has finally arrived on DEVONthink to go, DEVONthink’s mobile app, which unleashes new possibilities to work with your Personal Knowledge Management (PKM) system on the go.
How to get an RSS feed of your Mastodon bookmarks
The third-party service Mastodon Bookmark RSS allows you to subscribe to your Mastodon bookmarks via RSS, so you don’t forget to make use out of them. You can even integrate the feed into your favorite Zettelkasten apps such as DEVONthink and Obsidian.
Problems with large vaults in Obsidian
In the past few days I played a bit with Obsidian. Turns out that its iOS app has some serious problems with large vaults.
DEVONthink and privacy
One thing I really love about DEVONthink, is its high security and privacy measures regarding the synchronization of my notes across different devices. No other app that I have so far used offered such high standards.
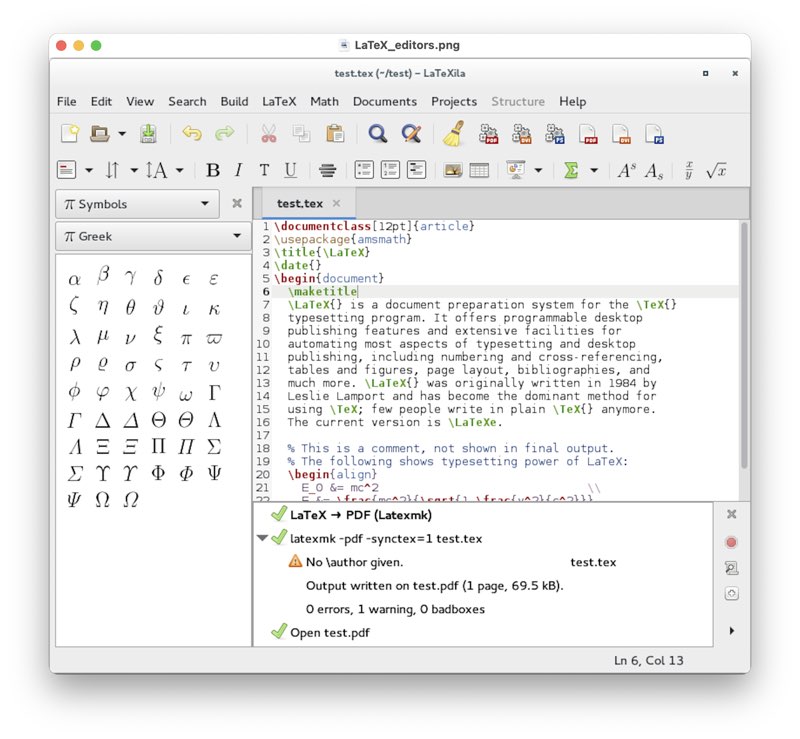
Using VS Code as LaTeX editor
It doesn’t take much to convert Visual Studio Code into a powerful LaTeX editor. Here are the necessary steps that enable full LaTeX support.
Hacks and extensions to improve your coding with Visual Studio Code
This curated list contains useful hacks and extensions to improve the overall coding performance with Visual Studio Code (VS Code).
How DEVONthink's auto-WikiLink feature changed my Zettelkasten workflow
DEVONthink’s automatic WikiLinks function is a powerful tool, both for discovering connections between notes – expected and unexpected ones – and for the automatized linking of these notes. In this post I briefly explain, how this feature has impacted my Zettelkasten workflow.
DEVONthink Markdown Table-of-Contents generator
I wrote a custom AppleScript for DEVONthink Markdown files, that bypasses the problem of broken links in the auto-generated Table-of-Contents (TOC) of MultiMarkdown (MMD).
Floating Back-to-top button for Markdown documents
You can quickly add a floating Back-to-top button to your Markdown documents in just two steps.
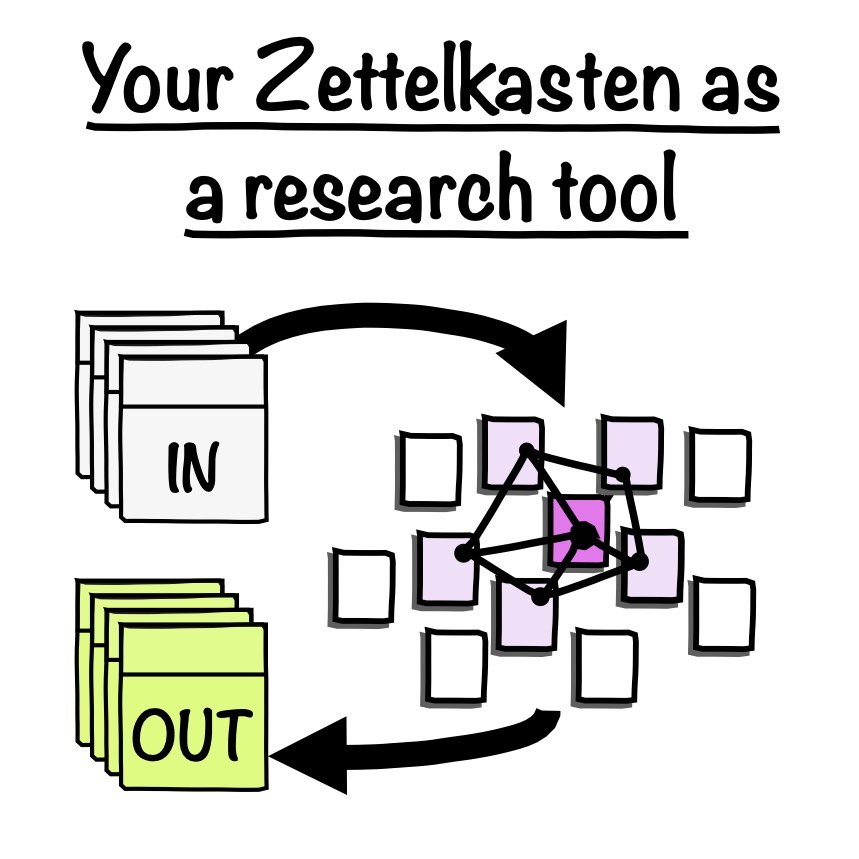
Use your Zettelkasten as a research, thinking and learning tool – Personal knowledge management as a system
In the last part of the series about personal knowledge management, we dive deeper into the Zettelkasten method and demonstrate, how to integrate all parts as an overall system into our research workflow.
Take smart notes with the Zettelkasten method
With the Zettelkasten method by Niklas Luhmann, we give the previously presented personal knowledge network a concrete shape and practical implementation. This is the second of three parts of the series about personal knowledge management.
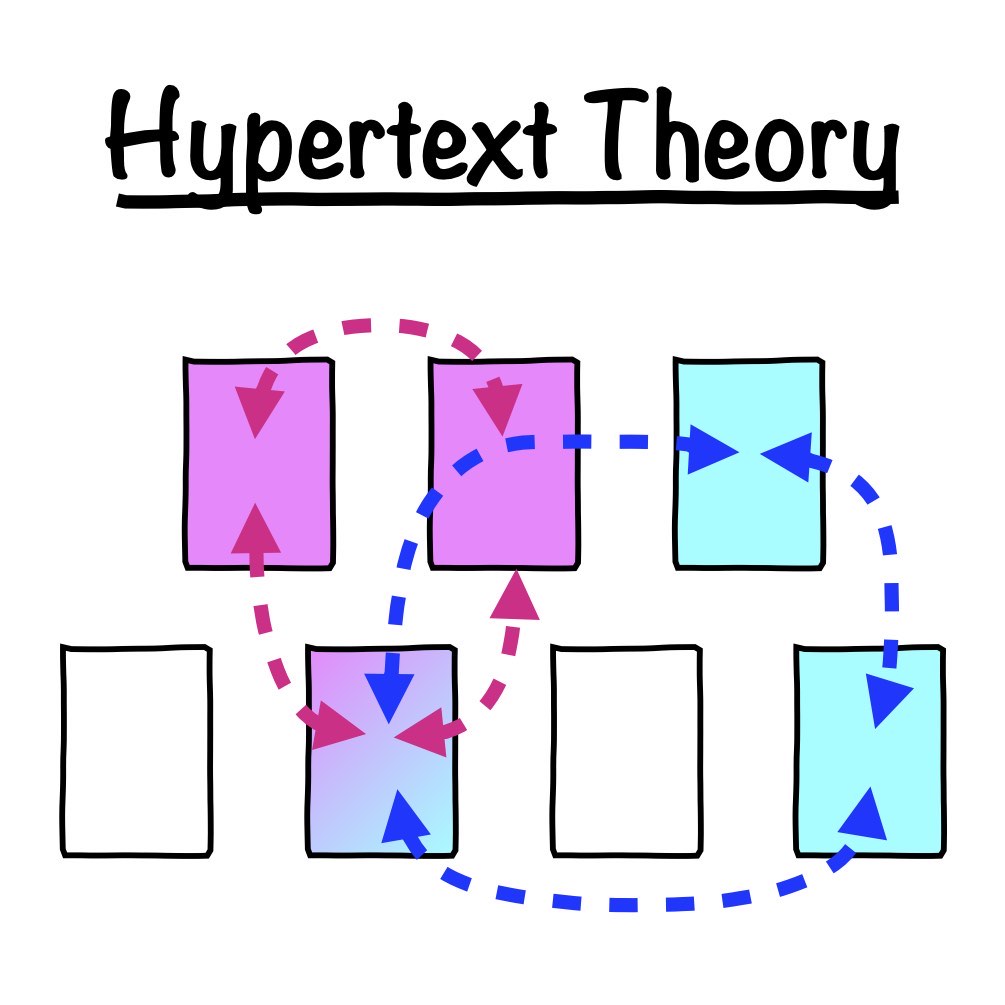
Don't take isolated notes, connect them! Vannevar Bush on building a self-organizing network of knowledge
In 1945, Vannevar Bush presented his concept of a self-organizing personal knowledge network by linking informational units with each other. This concept, that would later be known as the Hypertext concept or Hypertext theory, provides the theoretical base of the personal knowledge management system presented in the short series on that topic. This is the first of three parts of that series.
Boost your research with a smart personal knowledge management system
My next posts will be a short series about personal knowledge management and how it can be integrated as a holistic system into our overall research workflow. The system is based on the Hypertext Theory and the Zettelkasten method, and its core element is the personal note-taking process. We go step by step through all parts and see, how we can practically implement them into our daily research work.
Clean Thesis: A simple and elegant LaTeX thesis template
If you’re looking for some inspiration for your thesis, I just came across Clean Thesis by Ricardo Langner, a simple and elegant LaTeX template for thesis documents.
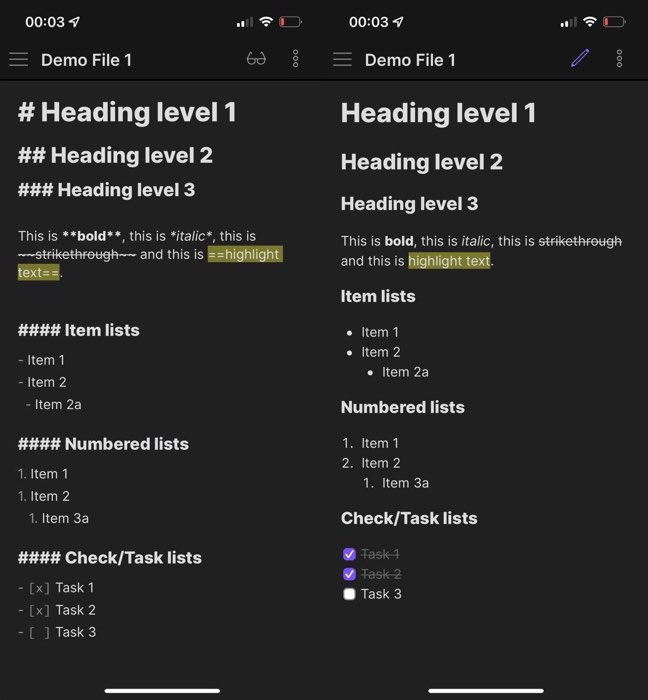
Using Markdown for note-taking
It might be a bit difficult to learn at the beginning, but there are several benefits of taking personal notes in Markdown. Here is why I switched.
strftime Cheat Sheet
Cheat Sheet on formatted date and time strings used, e.g., in Python, C/C++ or even on Jekyll websites by using Liquid tags.
Liquid Cheat Sheet
This Cheat Sheet gives an overview of Liquid syntax commands one might encounter while developing a Jekyll website.
Minimal Mistakes Cheat Sheet
A quick overview of available commands for creating content with the Minimal Mistakes Jekyll theme.
New Teaching Material: LaTeX Guide
I’ve added a LaTeX guide to the General Teaching Materials in the teaching section. It serves as a Getting started with LaTeX guide and as a LaTeX glossary.
#Neuroscience (40)
Distinguishing correlation from the coefficient of determination: Proper reporting of r and R²
I noticed that people sometimes report R² (‘R-squared’) instead of the Pearson correlation coefficient r when discussing the correlation between two variables. In the special case of a simple linear relationship this numerical equality is not strictly wrong, yet presenting R² as if it were the correlation coefficient might wrongly give the impression they are the same thing. In this post, we will therefore unpack the difference between these two measures, explain their mathematical definitions and proper usage discuss the best practices for when to use each in statistical reporting.
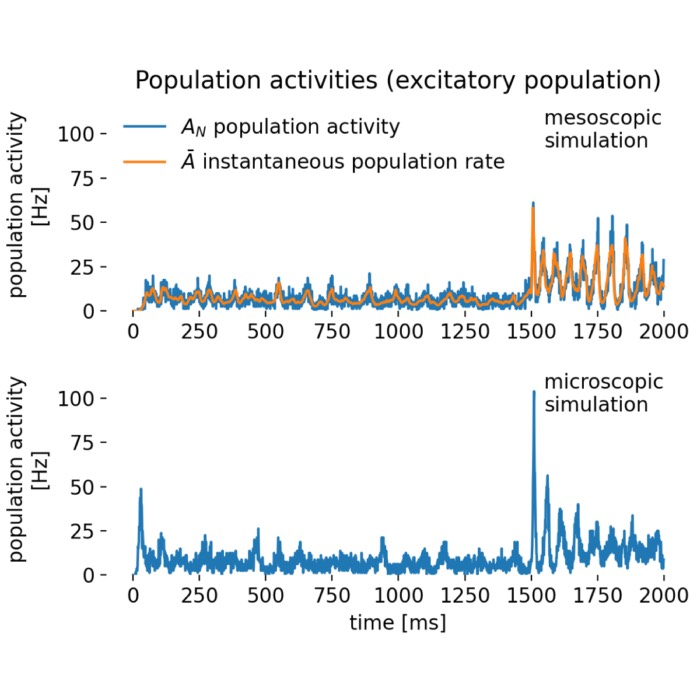
Rate models as a tool for studying collective neural activity
Rate models provide simplified representations of neural activity in which the precise spike timing of individual neurons is replaced by their average firing rate. This abstraction makes it possible to study the collective behavior of large neuronal populations and to analyze network dynamics in a tractable way. I recently played around with some rate models in Python, and in this post I’d like to share what I have learned so far about their implementation and utility.
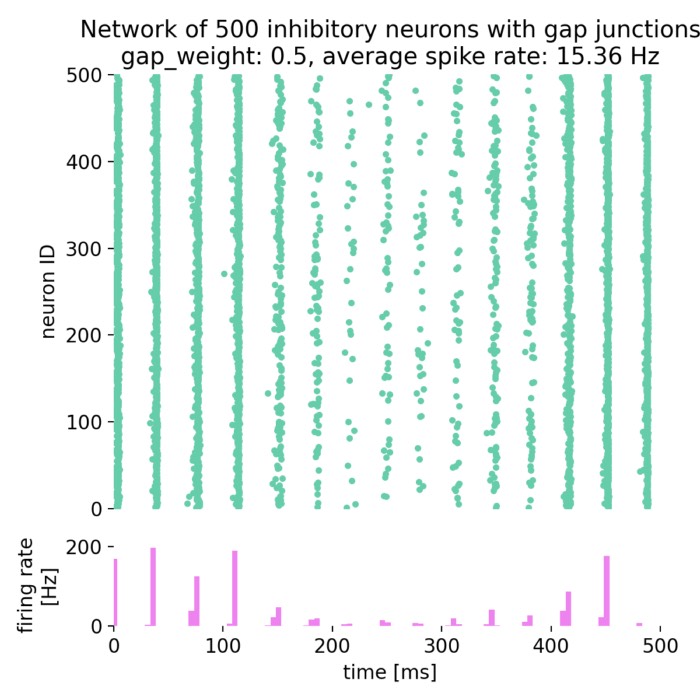
On the role of gap junctions in neural modelling: Network example
As a follow-up to our previous post on gap junctions, we will now explore how gap junctions can be implemented in a network of spiking neurons (SNN) using the NEST simulator. Gap junctions are electrical synapses that allow direct electrical communication between neurons, which can significantly influence the dynamics of neural networks.
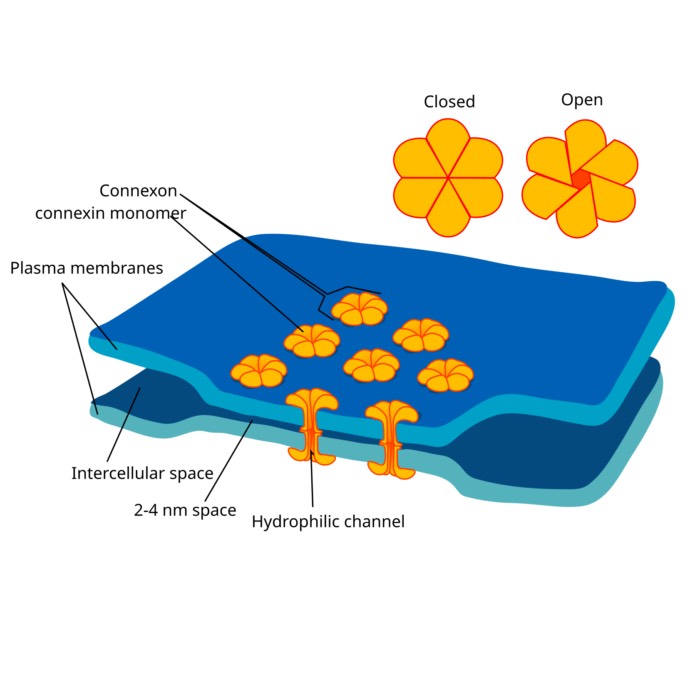
On the role of gap junctions in neural modelling
Gap junctions are specialized intercellular connections that facilitate direct electrical and chemical communication between neurons. Unlike synaptic transmission, which involves neurotransmitter release, gap junctions enable the direct passage of ions and small molecules through channels formed by connexins, leading to synchronized neuronal activity. In computational neuroscience, modeling gap junctions is crucial for understanding their role in neural network dynamics, synchronization, and various brain functions.
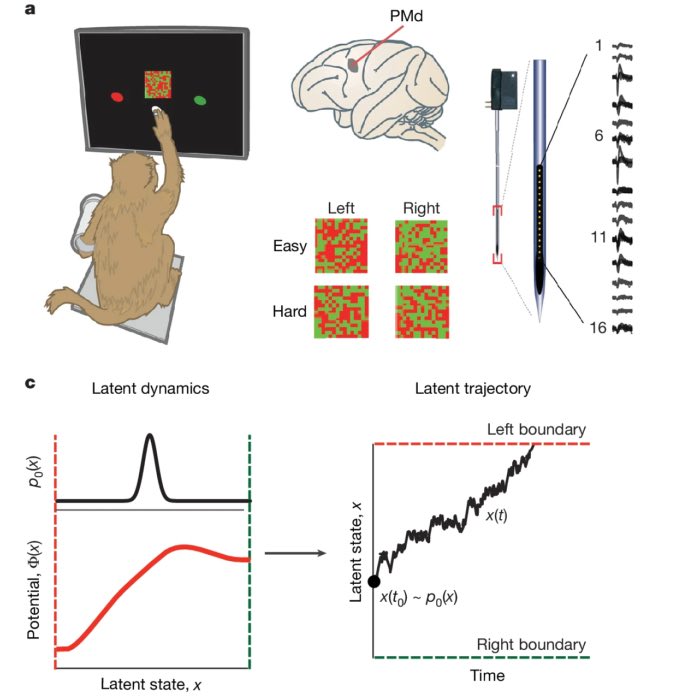
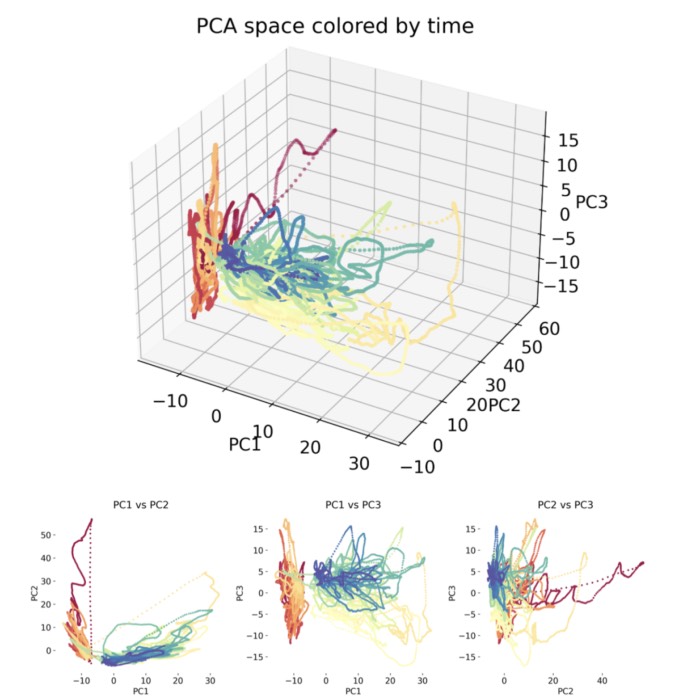
Shared dynamics, diverse responses: decoding decision-making in premotor cortex
Last week, I presented a recent study by Genkin et al., The dynamics and geometry of choice in the premotor cortex, in our Journal Club, and I found it conceptually compelling enough to summarize it here as well. The paper explores how perceptual decisions are encoded not in isolated neural responses but in population-wide latent dynamics. Traditionally, the neuroscience of decision-making has focused on ramping activity in individual neurons, heterogeneous peristimulus time histograms (PSTHs), and decoding strategies based on trial-averaged firing rates. In contrast, this work proposes that a shared low-dimensional decision variable evolves over time and explains the observed diversity in single-neuron responses. In our discussion, we focused on the paper’s central figures, using them to guide a step-by-step reconstruction of the study’s logic and findings.
New teaching material: Functional imaging data analysis – From calcium imaging to network dynamics
We have just completed our new course, Functional Imaging Data Analysis: From Calcium Imaging to Network Dynamics, for the first time as part of the Master of Neuroscience program. This course is now available freely online under ‘Teaching’, alongside my other open educational materials. All resources were created with a strict focus on open content and reproducibility, so that anyone interested can make full use of the lectures, figures, and example code without copyright concerns. Feel free to use and share it.
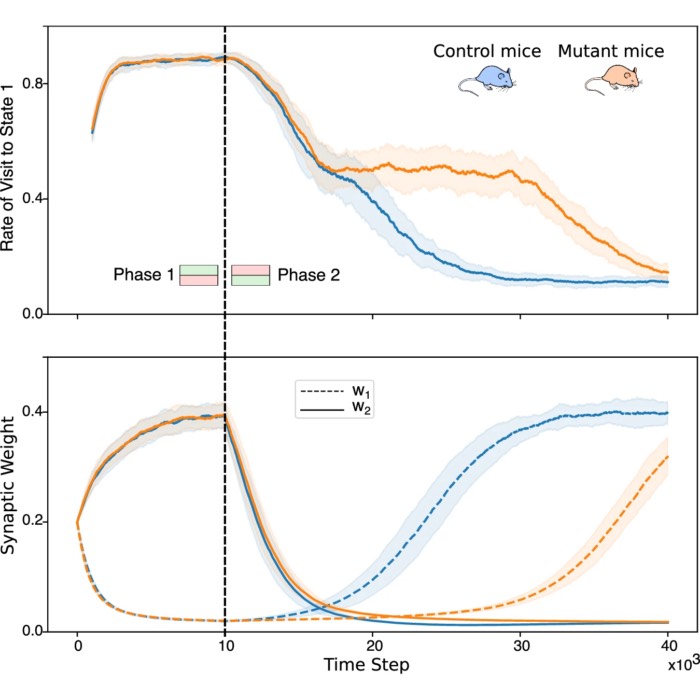
Astrocytes enhance plasticity response during reversal learning
Astrocytes, a type of glial cell traditionally considered support cells in the brain, are now recognized as active participants in synaptic plasticity and memory. I found this development particularly compelling and presented the following study in our Journal Club. The paper by Squadrani et al. (2024) explores the role of astrocyte-mediated D-serine regulation in modulating learning flexibility, particularly during reversal learning — the ability to adapt to changes in the environment. The work builds on prior experiments by Bohmbach et al. (2022), which identified an astrocyte-neuron feedback loop involving endocannabinoids and astrocytic D-serine release in the hippocampus.
New teaching material: Dimensionality reduction in neuroscience
We just completed a new two-day course on Dimensionality Reduction in Neuroscience, and I am pleased to announce that the full teaching material is now freely available under a Creative Commons (CC BY 4.0) license. This course is designed to provide an introductory overview of the application of dimensionality reduction techniques for neuroscientists and data scientists alike, focusing on how to handle the increasingly high-dimensional datasets generated by modern neuroscience research.
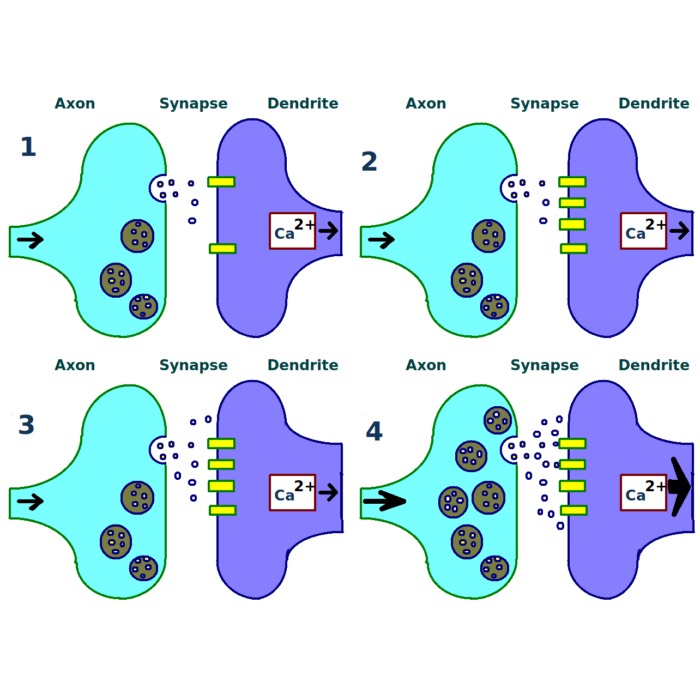
Long-term potentiation (LTP) and long-term depression (LTD)
Both long-term potentiation (LTP) and long-term depression (LTD) are forms of synaptic plasticity, which refers to the ability of synapses to change their strength over time. These processes are crucial for learning and memory, as they allow the brain to adapt to new information and experiences. Since we are often talking about both processes in the context of computational neuroscience, I thought it would be useful to provide a brief overview of biological mechanisms underlying these processes and their significance in the brain.
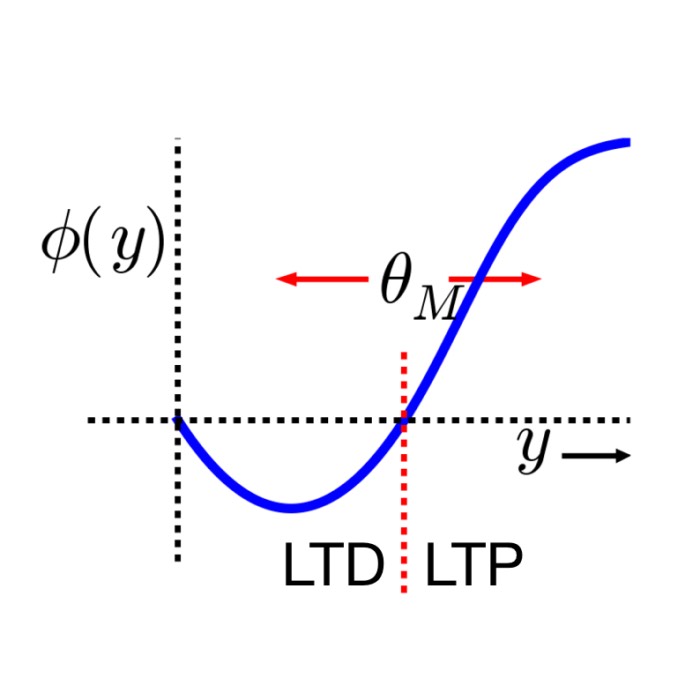
Bienenstock-Cooper-Munro (BCM) rule
The Bienenstock-Cooper-Munro (BCM) rule is a cornerstone in theoretical neuroscience, offering a comprehensive framework for understanding synaptic plasticity – the process by which connections between neurons are strengthened or weakened over time. Since its introduction in 1982, the BCM rule has provided critical insights into the mechanisms of learning and memory formation in the brain. In this post, we briefly explore and discuss the BCM rule, its theoretical foundations, mathematical formulations, and implications for neural plasticity.
Campbell and Siegert approximation for estimating the firing rate of a neuron
The Campbell and Siegert approximation is a method used in computational neuroscience to estimate the firing rate of a neuron given a certain input. This approximation is particularly useful for analyzing the firing behavior of neurons that follow a leaky integrate-and-fire (LIF) model or similar models under the influence of stochastic input currents.
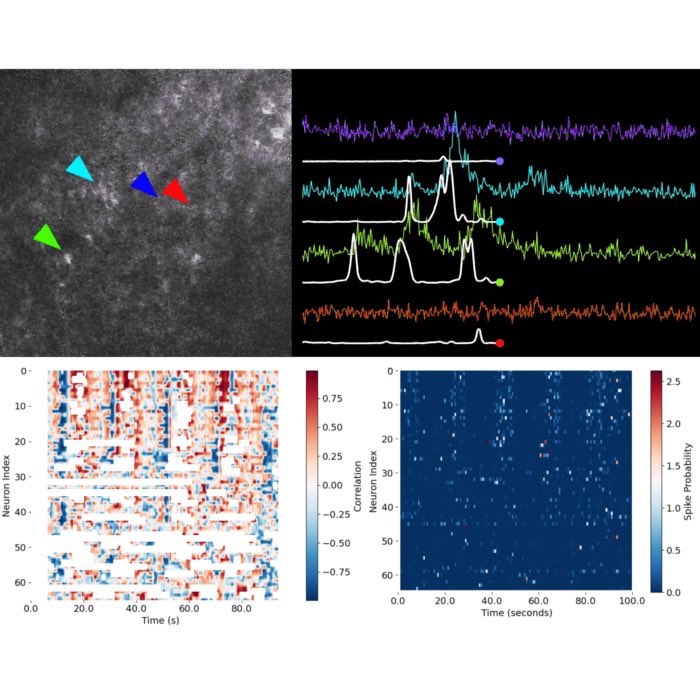
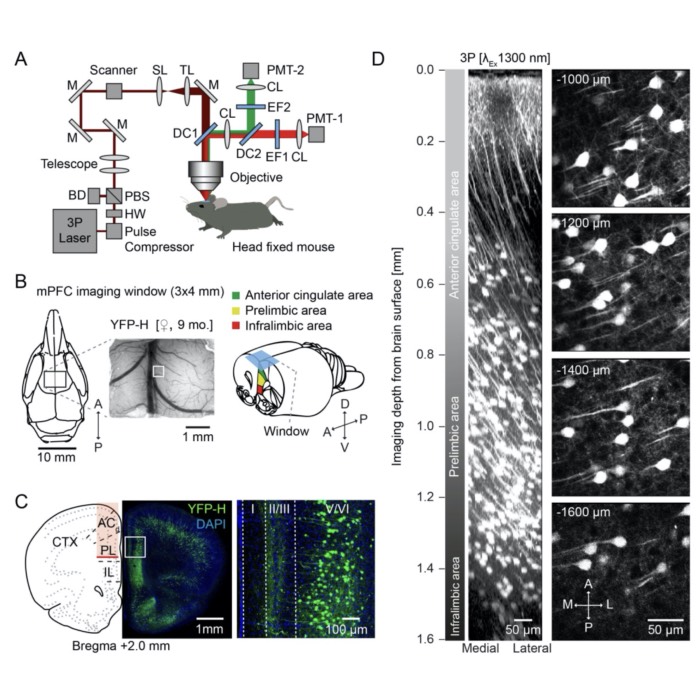
New preprint: Breaking new ground in brain imaging with three-photon microscopy
Our new preprint on Three-photon in vivo imaging of neurons and glia in the medial prefrontal cortex with sub-cellular resolution is out! In our study, we showcase the power of three-photon microscopy to probe deeper into the brain than ever before, achieving remarkable imaging depth and resolution in live, behaving animals.
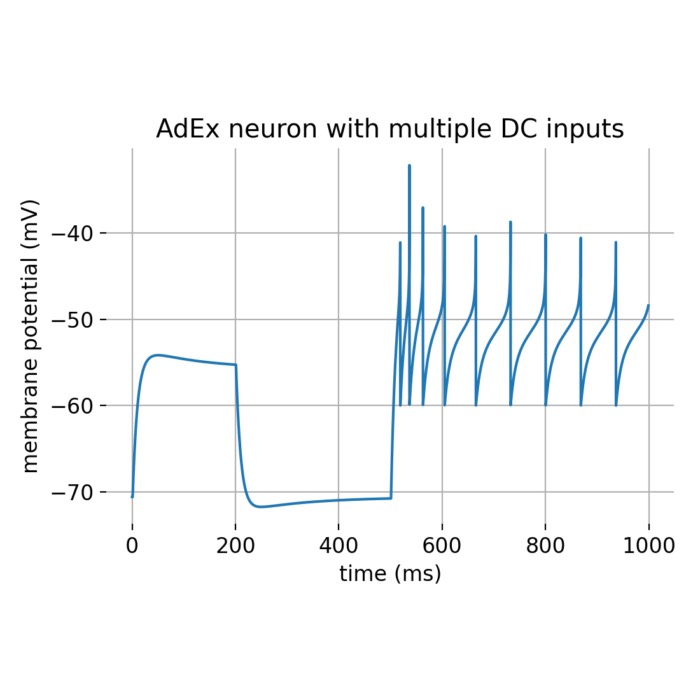
Exponential (EIF) and adaptive exponential Integrate-and-Fire (AdEx) model
The exponential Integrate-and-Fire (EIF) model is a simplified neuronal model that captures the essential dynamics of action potential generation. It extends the classical Integrate-and-Fire (IF) model by incorporating an exponential term to model the rapid rise of the membrane potential during spike initiation more accurately. The adaptive exponential Integrate-and-Fire (AdEx) model is a variant of the EIF model that includes an adaptation current to account for spike-frequency adaptation observed in real neurons. In this tutorial, we will explore the key features of the EIF and AdEx models and their applications in simulating neuronal dynamics.
Olfactory processing via spike-time based computation
In their work ‘Simple Networks for Spike-Timing-Based Computation, with Application to Olfactory Processing’ from 2003, Brody and Hopfield proposed a simple network model for olfactory processing. Brody and Hopfield showed how networks of spiking neurons (SNN) can be used to process temporal information based on computations on the timing of spikes rather than the rate of spikes. This is particularly relevant in the context of olfactory processing, where the timing of spikes in the olfactory bulb is crucial for encoding odor information. In this tutorial, we recapitulate the main concepts of Brody and Hopfield’s network using the NEST simulator.
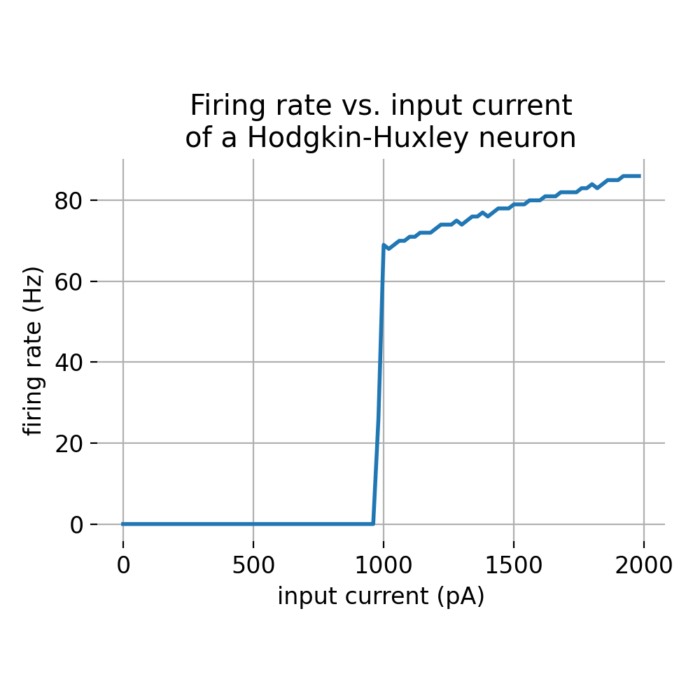
Frequency-current (f-I) curves
In this short tutorial, we will explore the concept of frequency-current (f-I) curves exemplified by the Hodgkin-Huxley neuron model. The f-I curve describes the relationship between the input current to a neuron and its firing rate. We will use the NEST simulator to simulate the behavior of a single Hodgkin-Huxley neuron and plot its f-I curve.
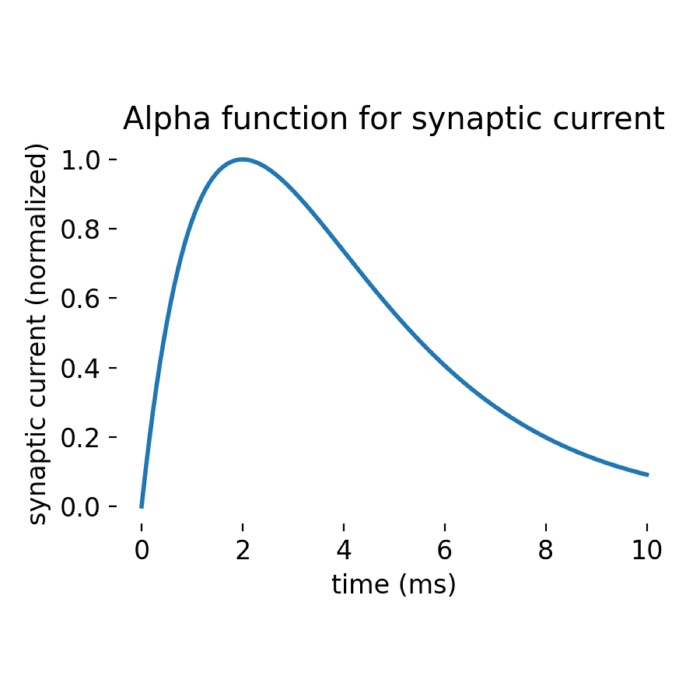
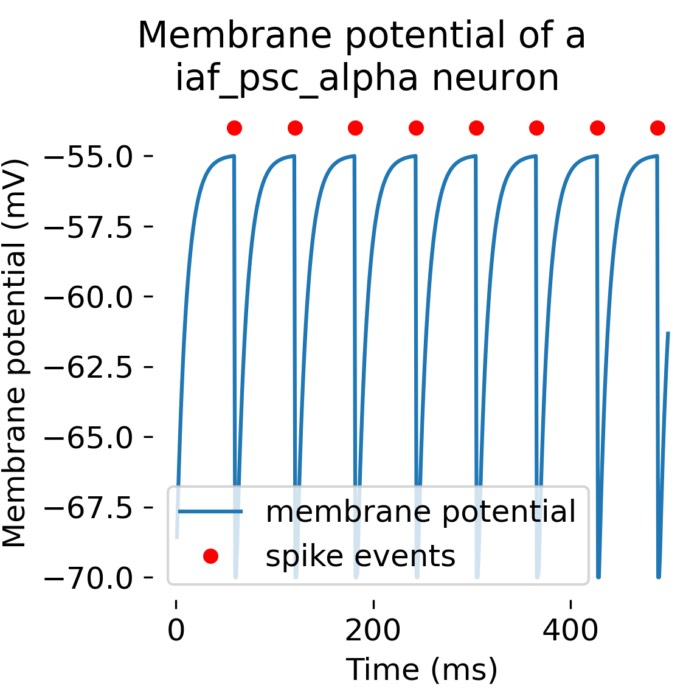
What are alpha-shaped post-synaptic currents?
In some recent posts, we have applied a specific type of integrate-and-fire neuron model, the
iaf_psc_alpha model implemented in the NEST simulator, to simulate the behavior of a single neuron or a population of neurons connected in a network. iaf_psc_alpha stands for ‘integrate-and-fire neuron with post-synaptic current shaped as an alpha function’. But what does ‘alpha-shaped current’ actually mean? In this short tutorial, we will explore the concept behind it.
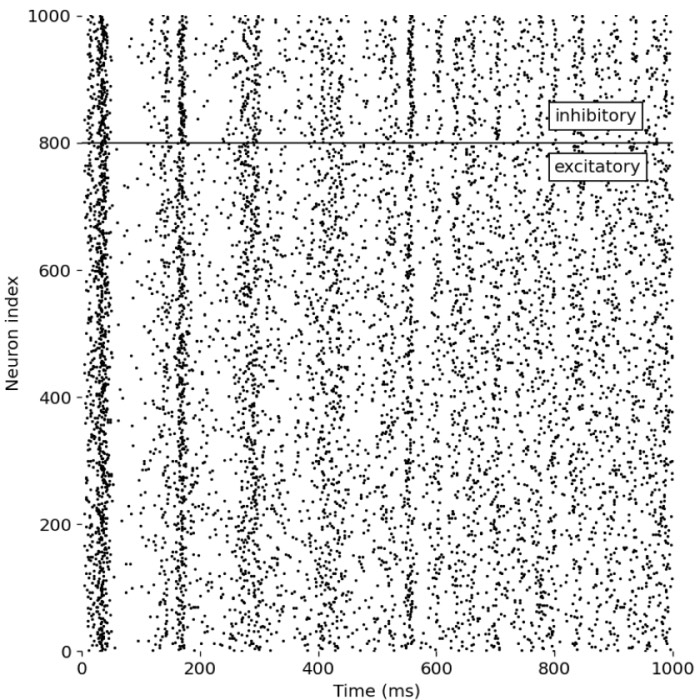
Example of a neuron driven by an inhibitory and excitatory neuron population
In this tutorial, we recap the NEST tutorial ‘Balanced neuron example’. We will simulate a neuron driven by an inhibitory and excitatory population of neurons firing Poisson spike trains. The goal is to find the optimal rate for the inhibitory population that will drive the neuron to fire at the same rate as the excitatory population. This short tutorial is quite interesting as it is a practical demonstration of using the NEST simulator to model complex neuronal dynamics.
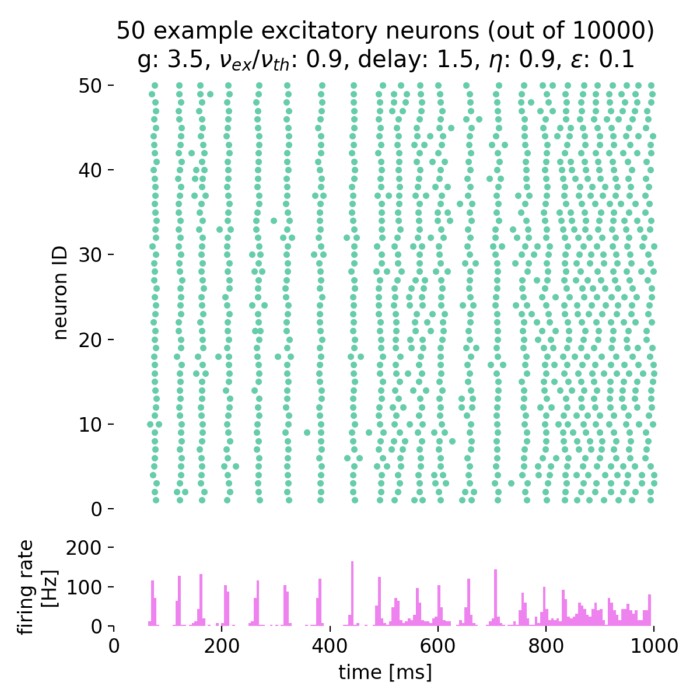
Brunel network: A comprehensive framework for studying neural network dynamics
In his work from 2000, Nicolas Brunel introduced a comprehensive framework for studying the dynamics of sparsely connected networks. The network is based on spiking neurons with random connectivity and differently balanced excitation and inhibition. It is characterized by a high level of sparseness and a low level of firing rates. The model is able to reproduce a wide range of neural dynamics, including both synchronized regular and asynchronous irregular activity as well as global oscillations. In this post, we summarize the essential concepts of that network and replicate the main results using the NEST simulator.
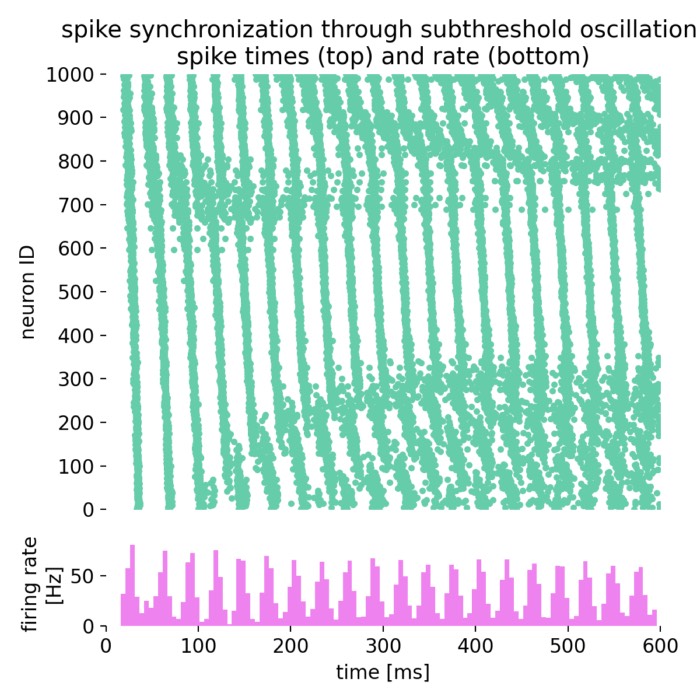
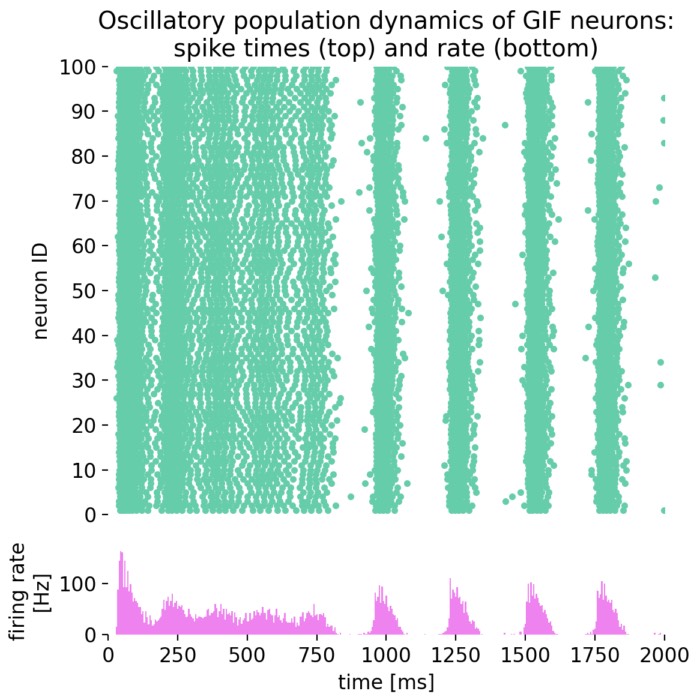
Oscillatory population dynamics of GIF neurons simulated with NEST
In this tutorial, we will explore the oscillatory population dynamics of generalized integrate-and-fire (GIF) neurons simulated with NEST. The GIF neuron model is a biophysically detailed model that captures the essential features of spiking neurons, including spike-frequency adaptation and dynamic threshold behavior. By simulating such a population of neurons, we can observe how these neurons interact and generate oscillatory firing patterns.
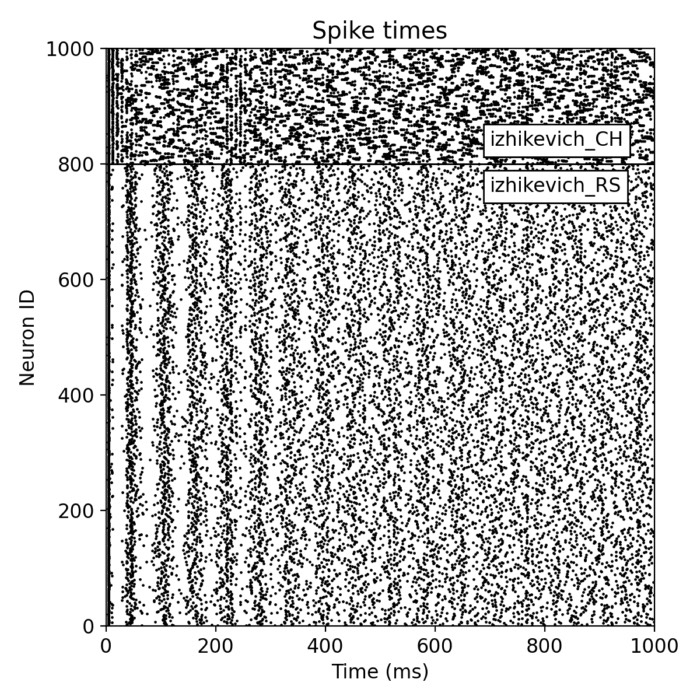
Izhikevich SNN simulated with NEST
In this post, we explore how easy it is to set up a large-scale, multi-population spiking neural network (SNN) with the NEST simulator. We simulate a simple SNN comprising two distinct populations of Izhikevich neurons, demonstrating the efficiency and flexibility of NEST and its capability to handle complex neural network simulations with ease.
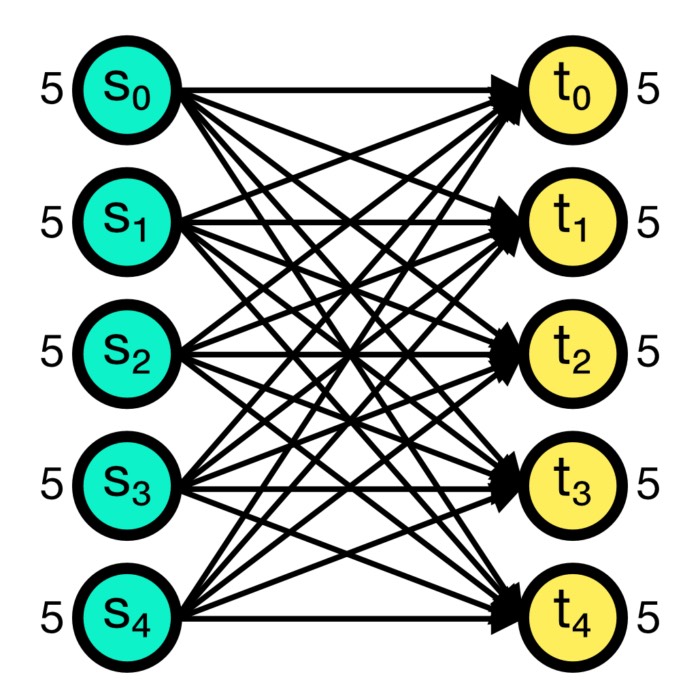
Connection concepts in NEST
In the previous post, we learned about the basic concepts of the NEST simulator and how to create a simple single neuron model. This time, we will take a closer look at the connection concepts in NEST, which are crucial for building more complex neural networks.
Step-by-step NEST single neuron simulation
While NEST is designed for large-scale simulations of neural spike networks, the underlying models are based on approximating the behavior of single neurons and synapses. Before using NEST for network simulations, it is probably helpful to first understand the basic functions of the software tool by modelling and studying the behavior of individual neurons. In this tutorial, you will learn about NEST’s concept of nodes and connections, how to set up a neuron model of your choice, how to change model parameters, which different stimulation paradigms are included in NEST and how to record and analyze the simulation results.
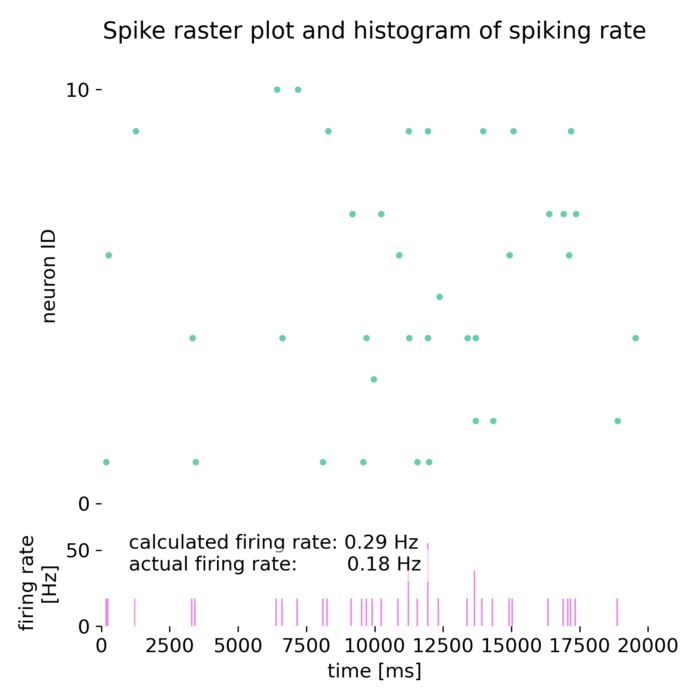
NEST simulator – A powerful tool for simulating large-scale spiking neural networks
The NEST simulator is a powerful software tool designed for simulating large-scale networks of spiking neurons (SNN). It has become an essential instrument in the field of computational neuroscience, providing the capability to model, simulate, and analyze the complex dynamics of neuronal systems. And it comes with a user-friendly Python interface, facilitating the construction of neuronal networks with minimal effort.
Simulating spiking neural networks with Izhikevich neurons
The Izhikevich neuron model that we have discussed earlier is known for its simplicity and computational efficiency as well as for its biological plausibility. The model is based on two coupled differential equations that describe the membrane potential and the recovery variable of a neuron. The model can reproduce a wide range of spiking behaviors observed in real neurons, such as regular spiking, fast spiking, chattering, and more. In this post, we explore how we can quickly set up a spiking neural network (SNN) simulation using the Izhikevich neuron model in Python.
Izhikevich model
Computational neuroscience utilizes mathematical models to understand the complex dynamics of neuronal activity. Among various neuron models, the Izhikevich model stands out for its ability to combine biological fidelity with computational efficiency. Developed by Eugene Izhikevich in 2003, this model simulates the spiking and bursting behavior of neurons with a remarkable balance between simplicity and biological relevance. In this post, we explore the properties of the Izhikevich model, examining its application and adaptability in simulating single neuron behaviors.
Hodgkin-Huxley model
An important step beyond simplified neuronal models is the Hodgkin-Huxley model. This model is based on the experimental data of Hodgkin and Huxley, who received the Nobel Prize in 1963 for their groundbreaking work. The model describes the dynamics of the membrane potential of a neuron by incorporating biophysiological properties instead of phenomenological descriptions. It is a cornerstone of computational neuroscience and has been used to study the dynamics of action potentials in neurons and the behavior of neural networks. In this post, we derive the Hodgkin-Huxley model step by step and provide a simple Python implementation.
FitzHugh-Nagumo model
In the previous post, we analyzed the dynamics of Van der Pol oscillator by using phase plane analysis. In this post, we will see, that this oscillator can be considered as a special case of another dynamical system, the FitzHugh-Nagumo model. The FitzHugh-Nagumo model is a simplified model used to describe the dynamics of the action potential in neurons. With a few modifications of the Van der Pol equations we can obtain the model’s ODE system. By again using phase plane analysis, we can then investigate how the dynamics of the system changes under these modifications.
Understanding Hebbian learning in Hopfield networks
Hopfield networks, a form of recurrent neural network (RNN), serve as a fundamental model for understanding associative memory and pattern recognition in computational neuroscience. Central to the operation of Hopfield networks is the Hebbian learning rule, an idea encapsulated by the maxim ‘neurons that fire together, wire together’. In this post, we explore the mathematical underpinnings of Hebbian learning within Hopfield networks, emphasizing its role in pattern recognition.
Integrate and Fire Model: A simple neuronal model
In this post we explore the Integrate-and-Fire model, a simplified representation of a neuron. We also run some simulations in Python to understand the model dynamics.
Assessing animal behavior with machine learning: New DeepLabCut tutorial
I have added a hands-on tutorial to the Assessing Animal Behavior lecture. The tutorial covers the GUI-based use of DeepLabCut, a popular open-source software package for markerless pose estimation of animals. The target group is neuroscience students with no or little programming knowledge. Feel free to share the tutorial with students or colleagues who might be interested in using DeepLabCut for their own projects.
Assessing animal behavior with machine learning
High-throughput and multi-modal behavior experiments, coupled with machine learning analysis, unlock valuable insights into complex systems by capturing diverse behavioral responses and deciphering hidden structures within high-dimensional datasets. I just completed a short introductory lecture on this topic, which is now available in the Teachings section.
Bioimage analysis with Napari
I’ve added new teaching material on using the free and open-source software (FOSS) Napari for bioimage analysis. Feel free to use and share it.
Mutual information and its relationship to information entropy
Mutual information is an essential measure in information theory that quantifies the statistical dependence between two random variables. Given its broad applicability, it has become an invaluable tool in diverse fields like machine learning, neuroscience, signal processing, and more. This post explores the mathematical foundations of mutual information and its relationship to information entropy. We will also demonstrate its implementation in some Python examples.
Information entropy
A fundamental concept that plays a pivotal role in quantifying the uncertainty or randomness of a set of data is the information entropy. Information entropy provides a measure of the average amount of information or surprise contained in a random variable. In this blog post, we explore its mathematical foundations and demonstrate its implementation in some Python examples.
How to read patch clamp recordings in WaveMetrics IGOR binary files (ibw) in Python
This is a mini tutorial on how to read patch clamp recordings in WaveMetrics IGOR binary files (*.ibw) in Python using the neo and igor packages.
New Teaching Material: Python Cheat Sheets
I’ve started a collection of various Python cheat sheets that contain some useful and commonly used commands and usage examples.
New Teaching Material: Statistical data analysis and basic time series analysis with Python
I’ve added two new tutorials in the teaching section on statistical data analysis and basic time series analysis with Python.
New Teaching Material: Analyzing IGOR binary files of patch clamp recordings
I’ve added a new tutorial in the teaching section on how to read and process IGOR binary files (ibw) of patch clamp recordings.
New Teaching Material: Fiji short course
There is a new tutorial in the Teaching Material. It’s a short Fiji tutorial on analyzing biomedical image data.
#Open Source (52)
Rate models as a tool for studying collective neural activity
Rate models provide simplified representations of neural activity in which the precise spike timing of individual neurons is replaced by their average firing rate. This abstraction makes it possible to study the collective behavior of large neuronal populations and to analyze network dynamics in a tractable way. I recently played around with some rate models in Python, and in this post I’d like to share what I have learned so far about their implementation and utility.
On the role of gap junctions in neural modelling: Network example
As a follow-up to our previous post on gap junctions, we will now explore how gap junctions can be implemented in a network of spiking neurons (SNN) using the NEST simulator. Gap junctions are electrical synapses that allow direct electrical communication between neurons, which can significantly influence the dynamics of neural networks.
On the role of gap junctions in neural modelling
Gap junctions are specialized intercellular connections that facilitate direct electrical and chemical communication between neurons. Unlike synaptic transmission, which involves neurotransmitter release, gap junctions enable the direct passage of ions and small molecules through channels formed by connexins, leading to synchronized neuronal activity. In computational neuroscience, modeling gap junctions is crucial for understanding their role in neural network dynamics, synchronization, and various brain functions.
Reflections on joining Bluesky: Opportunities and risks for the scientific community
Over the past two weeks, I have taken a closer look at Bluesky, exploring its features and dynamics through the lens of my own experience within the neuroscience community. So far, my impressions have been mixed: while some aspects of Bluesky are genuinely promising, others evoke certain concerns about the future of scientific communities on digital platforms. In this post, I would like to share a personal reflection on this recent shift, situating it within the broader context of academic social media migration.
New teaching material: Functional imaging data analysis – From calcium imaging to network dynamics
We have just completed our new course, Functional Imaging Data Analysis: From Calcium Imaging to Network Dynamics, for the first time as part of the Master of Neuroscience program. This course is now available freely online under ‘Teaching’, alongside my other open educational materials. All resources were created with a strict focus on open content and reproducibility, so that anyone interested can make full use of the lectures, figures, and example code without copyright concerns. Feel free to use and share it.
Miniforge: The minimal, open solution for institutional Python environments
In response to recent licensing changes by Anaconda, Inc., Miniforge has emerged as the recommended minimal installer for Python and scientific computing in academic and research institutions. Now bundling both conda and mamba, Miniforge replaces Miniconda and Mambaforge, ensuring high performance and broad package access via the conda-forge ecosystem. In this post, we briefly demonstrate how to install and migrate to Miniforge, along with troubleshooting tips for common issues in institutional settings.
Exploring connected notes: Local graph views for DEVONthink knowledge bases
DEVONthink has long been my preferred tool for managing personal knowledge. Its smart features, like automatic Wiki-links and AI-based classification, make it ideal for organizing interconnected notes. But these links often stay invisible without a visual layer. To address this, I developed a tool that generates interactive local graphs, embedded directly into each note. These graphs reveal how notes connect, highlighting clusters and patterns that text alone might miss. Fully local and integrated into DEVONthink 3, the system offers a lightweight way to navigate Markdown notes spatially. After refining it for my own workflow, I’m now sharing it for others who might benefit from clearer structure and better insight into their knowledge base.
New teaching material: Dimensionality reduction in neuroscience
We just completed a new two-day course on Dimensionality Reduction in Neuroscience, and I am pleased to announce that the full teaching material is now freely available under a Creative Commons (CC BY 4.0) license. This course is designed to provide an introductory overview of the application of dimensionality reduction techniques for neuroscientists and data scientists alike, focusing on how to handle the increasingly high-dimensional datasets generated by modern neuroscience research.
Long-term potentiation (LTP) and long-term depression (LTD)
Both long-term potentiation (LTP) and long-term depression (LTD) are forms of synaptic plasticity, which refers to the ability of synapses to change their strength over time. These processes are crucial for learning and memory, as they allow the brain to adapt to new information and experiences. Since we are often talking about both processes in the context of computational neuroscience, I thought it would be useful to provide a brief overview of biological mechanisms underlying these processes and their significance in the brain.
Bienenstock-Cooper-Munro (BCM) rule
The Bienenstock-Cooper-Munro (BCM) rule is a cornerstone in theoretical neuroscience, offering a comprehensive framework for understanding synaptic plasticity – the process by which connections between neurons are strengthened or weakened over time. Since its introduction in 1982, the BCM rule has provided critical insights into the mechanisms of learning and memory formation in the brain. In this post, we briefly explore and discuss the BCM rule, its theoretical foundations, mathematical formulations, and implications for neural plasticity.
Campbell and Siegert approximation for estimating the firing rate of a neuron
The Campbell and Siegert approximation is a method used in computational neuroscience to estimate the firing rate of a neuron given a certain input. This approximation is particularly useful for analyzing the firing behavior of neurons that follow a leaky integrate-and-fire (LIF) model or similar models under the influence of stochastic input currents.
Exponential (EIF) and adaptive exponential Integrate-and-Fire (AdEx) model
The exponential Integrate-and-Fire (EIF) model is a simplified neuronal model that captures the essential dynamics of action potential generation. It extends the classical Integrate-and-Fire (IF) model by incorporating an exponential term to model the rapid rise of the membrane potential during spike initiation more accurately. The adaptive exponential Integrate-and-Fire (AdEx) model is a variant of the EIF model that includes an adaptation current to account for spike-frequency adaptation observed in real neurons. In this tutorial, we will explore the key features of the EIF and AdEx models and their applications in simulating neuronal dynamics.
Olfactory processing via spike-time based computation
In their work ‘Simple Networks for Spike-Timing-Based Computation, with Application to Olfactory Processing’ from 2003, Brody and Hopfield proposed a simple network model for olfactory processing. Brody and Hopfield showed how networks of spiking neurons (SNN) can be used to process temporal information based on computations on the timing of spikes rather than the rate of spikes. This is particularly relevant in the context of olfactory processing, where the timing of spikes in the olfactory bulb is crucial for encoding odor information. In this tutorial, we recapitulate the main concepts of Brody and Hopfield’s network using the NEST simulator.
Frequency-current (f-I) curves
In this short tutorial, we will explore the concept of frequency-current (f-I) curves exemplified by the Hodgkin-Huxley neuron model. The f-I curve describes the relationship between the input current to a neuron and its firing rate. We will use the NEST simulator to simulate the behavior of a single Hodgkin-Huxley neuron and plot its f-I curve.
What are alpha-shaped post-synaptic currents?
In some recent posts, we have applied a specific type of integrate-and-fire neuron model, the
iaf_psc_alpha model implemented in the NEST simulator, to simulate the behavior of a single neuron or a population of neurons connected in a network. iaf_psc_alpha stands for ‘integrate-and-fire neuron with post-synaptic current shaped as an alpha function’. But what does ‘alpha-shaped current’ actually mean? In this short tutorial, we will explore the concept behind it.
Example of a neuron driven by an inhibitory and excitatory neuron population
In this tutorial, we recap the NEST tutorial ‘Balanced neuron example’. We will simulate a neuron driven by an inhibitory and excitatory population of neurons firing Poisson spike trains. The goal is to find the optimal rate for the inhibitory population that will drive the neuron to fire at the same rate as the excitatory population. This short tutorial is quite interesting as it is a practical demonstration of using the NEST simulator to model complex neuronal dynamics.
Brunel network: A comprehensive framework for studying neural network dynamics
In his work from 2000, Nicolas Brunel introduced a comprehensive framework for studying the dynamics of sparsely connected networks. The network is based on spiking neurons with random connectivity and differently balanced excitation and inhibition. It is characterized by a high level of sparseness and a low level of firing rates. The model is able to reproduce a wide range of neural dynamics, including both synchronized regular and asynchronous irregular activity as well as global oscillations. In this post, we summarize the essential concepts of that network and replicate the main results using the NEST simulator.
Oscillatory population dynamics of GIF neurons simulated with NEST
In this tutorial, we will explore the oscillatory population dynamics of generalized integrate-and-fire (GIF) neurons simulated with NEST. The GIF neuron model is a biophysically detailed model that captures the essential features of spiking neurons, including spike-frequency adaptation and dynamic threshold behavior. By simulating such a population of neurons, we can observe how these neurons interact and generate oscillatory firing patterns.
Izhikevich SNN simulated with NEST
In this post, we explore how easy it is to set up a large-scale, multi-population spiking neural network (SNN) with the NEST simulator. We simulate a simple SNN comprising two distinct populations of Izhikevich neurons, demonstrating the efficiency and flexibility of NEST and its capability to handle complex neural network simulations with ease.
Connection concepts in NEST
In the previous post, we learned about the basic concepts of the NEST simulator and how to create a simple single neuron model. This time, we will take a closer look at the connection concepts in NEST, which are crucial for building more complex neural networks.
Step-by-step NEST single neuron simulation
While NEST is designed for large-scale simulations of neural spike networks, the underlying models are based on approximating the behavior of single neurons and synapses. Before using NEST for network simulations, it is probably helpful to first understand the basic functions of the software tool by modelling and studying the behavior of individual neurons. In this tutorial, you will learn about NEST’s concept of nodes and connections, how to set up a neuron model of your choice, how to change model parameters, which different stimulation paradigms are included in NEST and how to record and analyze the simulation results.
NEST simulator – A powerful tool for simulating large-scale spiking neural networks
The NEST simulator is a powerful software tool designed for simulating large-scale networks of spiking neurons (SNN). It has become an essential instrument in the field of computational neuroscience, providing the capability to model, simulate, and analyze the complex dynamics of neuronal systems. And it comes with a user-friendly Python interface, facilitating the construction of neuronal networks with minimal effort.
Mamba vs. Conda: Unleashing lightning-fast Python package installations
If you’ve ever experienced the frustration of waiting for ages while installing Python packages with conda, there’s a game-changer I wish I’d heard about earlier: Mamba. This lightning-fast package manager surprised me with its incredible speed, making package installations a breeze. Here is my personal experience and why Mamba is the speed demon you may have been looking for.
Assessing animal behavior with machine learning: New DeepLabCut tutorial
I have added a hands-on tutorial to the Assessing Animal Behavior lecture. The tutorial covers the GUI-based use of DeepLabCut, a popular open-source software package for markerless pose estimation of animals. The target group is neuroscience students with no or little programming knowledge. Feel free to share the tutorial with students or colleagues who might be interested in using DeepLabCut for their own projects.
Assessing animal behavior with machine learning
High-throughput and multi-modal behavior experiments, coupled with machine learning analysis, unlock valuable insights into complex systems by capturing diverse behavioral responses and deciphering hidden structures within high-dimensional datasets. I just completed a short introductory lecture on this topic, which is now available in the Teachings section.
Bioimage analysis with Napari
I’ve added new teaching material on using the free and open-source software (FOSS) Napari for bioimage analysis. Feel free to use and share it.
How to get an RSS feed of your Mastodon bookmarks
The third-party service Mastodon Bookmark RSS allows you to subscribe to your Mastodon bookmarks via RSS, so you don’t forget to make use out of them. You can even integrate the feed into your favorite Zettelkasten apps such as DEVONthink and Obsidian.
Bio-image registration with Python
Which method works best for which registration problem? In this tutorial we compare different methods for the registration of bio-images using Python.
Moving a Mastodon account to another server
I recently moved my Mastodon account to a new server, including all my followers. I was surprised, how easy and seamless it worked. Here is a how-to, summarizing the migration steps.
I'm on Mastodon
Mastodon is not just a Twitter alternative. It’s a free and open-source social media platform of its own kind. Here is my story how I got there.
How to run PyTorch on the M1 Mac GPU
As for TensorFlow, it takes only a few steps to enable a Mac with M1 chip (Apple silicon) for machine learning tasks in Python with PyTorch.
How to run TensorFlow on the M1 Mac GPU
In just a few steps you can enable a Mac with M1 chip (Apple silicon) for machine learning tasks in Python with TensorFlow.
Is there a difference between miniconda and miniforge?
Simply said: not really. Miniconda is the company driven minimal conda installer, while miniforge is its community driven variant. In the end, you’ll get the same minimal conda installation on your machine – with a minor difference.
Hacks and extensions to improve your coding with Visual Studio Code
This curated list contains useful hacks and extensions to improve the overall coding performance with Visual Studio Code (VS Code).
Setting up Visual Studio Code for Python
In just a few steps you can turn Visual Studio Code (VS Code) into a powerful Python editor for both pure Python code and Jupyter Notebooks.
Enable interactive plots and other plot modes in Jupyter notebooks
Learn how to enable interactive, static and stand-alone window plots in Jupyter notebooks with the magic command
%matplotlib.
Enable code folding in JupyterLab
Learn how to enable code folding in JupyterLab for both, Jupyter Notebooks and pure Python scripts.
How to create and apply a requirements.txt file in Python
Learn how to install Python packages with a requirements.txt file and how to create one yourself.
Virtual environments with venv
In addition to conda’s
create command, Python’s built-in venv command offers another way for creating virtual environments.
Using pip to install Python packages
pip is another package installer for Python. Learn how to use it for installing and managing Python packages in your projects.
How to install and run Python code from GitHub
Learn how to install code from GitHub, that is, e.g., not (yet) available via conda or pip.
A minimal Python installation with miniconda
Learn how to install miniconda to have a quick and minimal Python installation on any operating system. Also learn how to use conda to create and manage virtual environments, install packages, run Python scripts and run Jupyter Notebooks and JupyterLab.
Stable installation of Napari on a M1 Mac
In case you’re having problems installing Napari on your M1 Mac, try to install it from conda instead of pip.
Using Zarr for images – The OME-ZARR standard
As for any other NumPy array, we can use the Zarr file format to store image files. In this post we additionally explore the NGFF (next-generation file format) OME-ZARR standard.
Zarr – or: How to save NumPy arrays
What is Zarr and why is it probably the most suitable file format for saving NumPy arrays?
Variable Explorer in Jupyter Notebooks
Extend your Jupyter environment with Notebook Extensions and enable, e.g., the option to explore your currently defined variables in a running Jupyter session.
Clean Thesis: A simple and elegant LaTeX thesis template
If you’re looking for some inspiration for your thesis, I just came across Clean Thesis by Ricardo Langner, a simple and elegant LaTeX template for thesis documents.
My website is now completely cookie-free
I made several changes to my website to further increase the privacy protection. As a result, it runs now completely without cookies.
#Personal Knowledge Management (19)
Exploring connected notes: Local graph views for DEVONthink knowledge bases
DEVONthink has long been my preferred tool for managing personal knowledge. Its smart features, like automatic Wiki-links and AI-based classification, make it ideal for organizing interconnected notes. But these links often stay invisible without a visual layer. To address this, I developed a tool that generates interactive local graphs, embedded directly into each note. These graphs reveal how notes connect, highlighting clusters and patterns that text alone might miss. Fully local and integrated into DEVONthink 3, the system offers a lightweight way to navigate Markdown notes spatially. After refining it for my own workflow, I’m now sharing it for others who might benefit from clearer structure and better insight into their knowledge base.
Bridging ideas on the go: WikiLinks come to DEVONthink To Go
The WikiLinks feature has finally arrived on DEVONthink to go, DEVONthink’s mobile app, which unleashes new possibilities to work with your Personal Knowledge Management (PKM) system on the go.
How to get an RSS feed of your Mastodon bookmarks
The third-party service Mastodon Bookmark RSS allows you to subscribe to your Mastodon bookmarks via RSS, so you don’t forget to make use out of them. You can even integrate the feed into your favorite Zettelkasten apps such as DEVONthink and Obsidian.
Problems with large vaults in Obsidian
In the past few days I played a bit with Obsidian. Turns out that its iOS app has some serious problems with large vaults.
DEVONthink and privacy
One thing I really love about DEVONthink, is its high security and privacy measures regarding the synchronization of my notes across different devices. No other app that I have so far used offered such high standards.
How DEVONthink's auto-WikiLink feature changed my Zettelkasten workflow
DEVONthink’s automatic WikiLinks function is a powerful tool, both for discovering connections between notes – expected and unexpected ones – and for the automatized linking of these notes. In this post I briefly explain, how this feature has impacted my Zettelkasten workflow.
DEVONthink Markdown Table-of-Contents generator
I wrote a custom AppleScript for DEVONthink Markdown files, that bypasses the problem of broken links in the auto-generated Table-of-Contents (TOC) of MultiMarkdown (MMD).
Floating Back-to-top button for Markdown documents
You can quickly add a floating Back-to-top button to your Markdown documents in just two steps.
Use your Zettelkasten as a research, thinking and learning tool – Personal knowledge management as a system
In the last part of the series about personal knowledge management, we dive deeper into the Zettelkasten method and demonstrate, how to integrate all parts as an overall system into our research workflow.
Take smart notes with the Zettelkasten method
With the Zettelkasten method by Niklas Luhmann, we give the previously presented personal knowledge network a concrete shape and practical implementation. This is the second of three parts of the series about personal knowledge management.
Don't take isolated notes, connect them! Vannevar Bush on building a self-organizing network of knowledge
In 1945, Vannevar Bush presented his concept of a self-organizing personal knowledge network by linking informational units with each other. This concept, that would later be known as the Hypertext concept or Hypertext theory, provides the theoretical base of the personal knowledge management system presented in the short series on that topic. This is the first of three parts of that series.
Boost your research with a smart personal knowledge management system
My next posts will be a short series about personal knowledge management and how it can be integrated as a holistic system into our overall research workflow. The system is based on the Hypertext Theory and the Zettelkasten method, and its core element is the personal note-taking process. We go step by step through all parts and see, how we can practically implement them into our daily research work.
Using Markdown for note-taking
It might be a bit difficult to learn at the beginning, but there are several benefits of taking personal notes in Markdown. Here is why I switched.
#Personal Opinion (14)
Reflections on joining Bluesky: Opportunities and risks for the scientific community
Over the past two weeks, I have taken a closer look at Bluesky, exploring its features and dynamics through the lens of my own experience within the neuroscience community. So far, my impressions have been mixed: while some aspects of Bluesky are genuinely promising, others evoke certain concerns about the future of scientific communities on digital platforms. In this post, I would like to share a personal reflection on this recent shift, situating it within the broader context of academic social media migration.
Visualizing Occam's Razor through machine learning
Here, we illustrate the concept of Occam’s Razor, a principle advocating for simplicity, by examining its manifestation in the domain of machine learning using Python.
Zen and natural sciences
In this post, I broaden the scope and explore the intersections of Zen and natural sciences more generally.
The Zen of Python
The connection between Zen and programming is not a subjective one at all. For instance, Python has built it directly into its core programming, known as The Zen of Python.
DEVONthink and privacy
One thing I really love about DEVONthink, is its high security and privacy measures regarding the synchronization of my notes across different devices. No other app that I have so far used offered such high standards.
I'm on Mastodon
Mastodon is not just a Twitter alternative. It’s a free and open-source social media platform of its own kind. Here is my story how I got there.
Laying off thousands of employees: Not okay! How to delete a Twitter account
Putting thousands of people on the street is anything else than cool. Here is how to fix it.
The quickest way to find help for Python commands: The help() command
Python’s built-in help system is probably the fastest way, to quickly look up Python commands and their syntax. It works without leaving your Python environment and is fully offline available.
On teaching
I strongly believe that teaching is not a unidirectional thing, but both sides, the participants and the teacher benefit from it. This is a personal comment on teaching.
On website subscriptions via RSS and Atom feeds
Personal opinion on how to create and maintain personal news feeds beyond the dependence on big social media and tech companies.
#Photography (1)
#Physics (3)
The two-body problem
The two-body system is a classical problem in physics. It describes the motion of two massive objects that are influenced by their mutual gravitational attraction. The two-body problem is a special case of the n-body problem, which describes the motion of two objects that are influenced by their mutual gravitational attraction. In this post, we make use of Runge-Kutta methods to solve the according equations of motion and simulate the trajectories of artificial satellites around the Earth.
Solving the Lorenz system using Runge-Kutta methods
In my previous post, I introduced the Runge-Kutta methods for numerically solving ordinary differential equations (ODEs), that are challenging to solve analytically. In this post, we apply the Runge-Kutta methods to solve the Lorenz system. The Lorenz system is a set of differential equations known for its chaotic behavior and non-linear dynamics. By utilizing the Runge-Kutta methods, we can effectively simulate and analyze the intricate dynamics of this system.
Earth's dipolar magnetic field
In physics and computational mathematics, numerical methods for solving ordinary differential equations (ODEs) are of central importance. Among these, the family of Runge-Kutta methods stands out due to its versatility and robustness. In this post we compare the first four orders of the Runge-Kutta methods, namely RK1 (Euler’s method), RK2, RK3, and RK4.
#Privacy (3)
DEVONthink and privacy
One thing I really love about DEVONthink, is its high security and privacy measures regarding the synchronization of my notes across different devices. No other app that I have so far used offered such high standards.
My website is now completely cookie-free
I made several changes to my website to further increase the privacy protection. As a result, it runs now completely without cookies.
On website subscriptions via RSS and Atom feeds
Personal opinion on how to create and maintain personal news feeds beyond the dependence on big social media and tech companies.
#Python (96)
Distinguishing correlation from the coefficient of determination: Proper reporting of r and R²
I noticed that people sometimes report R² (‘R-squared’) instead of the Pearson correlation coefficient r when discussing the correlation between two variables. In the special case of a simple linear relationship this numerical equality is not strictly wrong, yet presenting R² as if it were the correlation coefficient might wrongly give the impression they are the same thing. In this post, we will therefore unpack the difference between these two measures, explain their mathematical definitions and proper usage discuss the best practices for when to use each in statistical reporting.
Rate models as a tool for studying collective neural activity
Rate models provide simplified representations of neural activity in which the precise spike timing of individual neurons is replaced by their average firing rate. This abstraction makes it possible to study the collective behavior of large neuronal populations and to analyze network dynamics in a tractable way. I recently played around with some rate models in Python, and in this post I’d like to share what I have learned so far about their implementation and utility.
On the role of gap junctions in neural modelling: Network example
As a follow-up to our previous post on gap junctions, we will now explore how gap junctions can be implemented in a network of spiking neurons (SNN) using the NEST simulator. Gap junctions are electrical synapses that allow direct electrical communication between neurons, which can significantly influence the dynamics of neural networks.
On the role of gap junctions in neural modelling
Gap junctions are specialized intercellular connections that facilitate direct electrical and chemical communication between neurons. Unlike synaptic transmission, which involves neurotransmitter release, gap junctions enable the direct passage of ions and small molecules through channels formed by connexins, leading to synchronized neuronal activity. In computational neuroscience, modeling gap junctions is crucial for understanding their role in neural network dynamics, synchronization, and various brain functions.
New teaching material: Functional imaging data analysis – From calcium imaging to network dynamics
We have just completed our new course, Functional Imaging Data Analysis: From Calcium Imaging to Network Dynamics, for the first time as part of the Master of Neuroscience program. This course is now available freely online under ‘Teaching’, alongside my other open educational materials. All resources were created with a strict focus on open content and reproducibility, so that anyone interested can make full use of the lectures, figures, and example code without copyright concerns. Feel free to use and share it.
Miniforge: The minimal, open solution for institutional Python environments
In response to recent licensing changes by Anaconda, Inc., Miniforge has emerged as the recommended minimal installer for Python and scientific computing in academic and research institutions. Now bundling both conda and mamba, Miniforge replaces Miniconda and Mambaforge, ensuring high performance and broad package access via the conda-forge ecosystem. In this post, we briefly demonstrate how to install and migrate to Miniforge, along with troubleshooting tips for common issues in institutional settings.
Exploring connected notes: Local graph views for DEVONthink knowledge bases
DEVONthink has long been my preferred tool for managing personal knowledge. Its smart features, like automatic Wiki-links and AI-based classification, make it ideal for organizing interconnected notes. But these links often stay invisible without a visual layer. To address this, I developed a tool that generates interactive local graphs, embedded directly into each note. These graphs reveal how notes connect, highlighting clusters and patterns that text alone might miss. Fully local and integrated into DEVONthink 3, the system offers a lightweight way to navigate Markdown notes spatially. After refining it for my own workflow, I’m now sharing it for others who might benefit from clearer structure and better insight into their knowledge base.
New teaching material: Dimensionality reduction in neuroscience
We just completed a new two-day course on Dimensionality Reduction in Neuroscience, and I am pleased to announce that the full teaching material is now freely available under a Creative Commons (CC BY 4.0) license. This course is designed to provide an introductory overview of the application of dimensionality reduction techniques for neuroscientists and data scientists alike, focusing on how to handle the increasingly high-dimensional datasets generated by modern neuroscience research.
Long-term potentiation (LTP) and long-term depression (LTD)
Both long-term potentiation (LTP) and long-term depression (LTD) are forms of synaptic plasticity, which refers to the ability of synapses to change their strength over time. These processes are crucial for learning and memory, as they allow the brain to adapt to new information and experiences. Since we are often talking about both processes in the context of computational neuroscience, I thought it would be useful to provide a brief overview of biological mechanisms underlying these processes and their significance in the brain.
Bienenstock-Cooper-Munro (BCM) rule
The Bienenstock-Cooper-Munro (BCM) rule is a cornerstone in theoretical neuroscience, offering a comprehensive framework for understanding synaptic plasticity – the process by which connections between neurons are strengthened or weakened over time. Since its introduction in 1982, the BCM rule has provided critical insights into the mechanisms of learning and memory formation in the brain. In this post, we briefly explore and discuss the BCM rule, its theoretical foundations, mathematical formulations, and implications for neural plasticity.
Campbell and Siegert approximation for estimating the firing rate of a neuron
The Campbell and Siegert approximation is a method used in computational neuroscience to estimate the firing rate of a neuron given a certain input. This approximation is particularly useful for analyzing the firing behavior of neurons that follow a leaky integrate-and-fire (LIF) model or similar models under the influence of stochastic input currents.
Exponential (EIF) and adaptive exponential Integrate-and-Fire (AdEx) model
The exponential Integrate-and-Fire (EIF) model is a simplified neuronal model that captures the essential dynamics of action potential generation. It extends the classical Integrate-and-Fire (IF) model by incorporating an exponential term to model the rapid rise of the membrane potential during spike initiation more accurately. The adaptive exponential Integrate-and-Fire (AdEx) model is a variant of the EIF model that includes an adaptation current to account for spike-frequency adaptation observed in real neurons. In this tutorial, we will explore the key features of the EIF and AdEx models and their applications in simulating neuronal dynamics.
Olfactory processing via spike-time based computation
In their work ‘Simple Networks for Spike-Timing-Based Computation, with Application to Olfactory Processing’ from 2003, Brody and Hopfield proposed a simple network model for olfactory processing. Brody and Hopfield showed how networks of spiking neurons (SNN) can be used to process temporal information based on computations on the timing of spikes rather than the rate of spikes. This is particularly relevant in the context of olfactory processing, where the timing of spikes in the olfactory bulb is crucial for encoding odor information. In this tutorial, we recapitulate the main concepts of Brody and Hopfield’s network using the NEST simulator.
Frequency-current (f-I) curves
In this short tutorial, we will explore the concept of frequency-current (f-I) curves exemplified by the Hodgkin-Huxley neuron model. The f-I curve describes the relationship between the input current to a neuron and its firing rate. We will use the NEST simulator to simulate the behavior of a single Hodgkin-Huxley neuron and plot its f-I curve.
What are alpha-shaped post-synaptic currents?
In some recent posts, we have applied a specific type of integrate-and-fire neuron model, the
iaf_psc_alpha model implemented in the NEST simulator, to simulate the behavior of a single neuron or a population of neurons connected in a network. iaf_psc_alpha stands for ‘integrate-and-fire neuron with post-synaptic current shaped as an alpha function’. But what does ‘alpha-shaped current’ actually mean? In this short tutorial, we will explore the concept behind it.
Example of a neuron driven by an inhibitory and excitatory neuron population
In this tutorial, we recap the NEST tutorial ‘Balanced neuron example’. We will simulate a neuron driven by an inhibitory and excitatory population of neurons firing Poisson spike trains. The goal is to find the optimal rate for the inhibitory population that will drive the neuron to fire at the same rate as the excitatory population. This short tutorial is quite interesting as it is a practical demonstration of using the NEST simulator to model complex neuronal dynamics.
Brunel network: A comprehensive framework for studying neural network dynamics
In his work from 2000, Nicolas Brunel introduced a comprehensive framework for studying the dynamics of sparsely connected networks. The network is based on spiking neurons with random connectivity and differently balanced excitation and inhibition. It is characterized by a high level of sparseness and a low level of firing rates. The model is able to reproduce a wide range of neural dynamics, including both synchronized regular and asynchronous irregular activity as well as global oscillations. In this post, we summarize the essential concepts of that network and replicate the main results using the NEST simulator.
Oscillatory population dynamics of GIF neurons simulated with NEST
In this tutorial, we will explore the oscillatory population dynamics of generalized integrate-and-fire (GIF) neurons simulated with NEST. The GIF neuron model is a biophysically detailed model that captures the essential features of spiking neurons, including spike-frequency adaptation and dynamic threshold behavior. By simulating such a population of neurons, we can observe how these neurons interact and generate oscillatory firing patterns.
Izhikevich SNN simulated with NEST
In this post, we explore how easy it is to set up a large-scale, multi-population spiking neural network (SNN) with the NEST simulator. We simulate a simple SNN comprising two distinct populations of Izhikevich neurons, demonstrating the efficiency and flexibility of NEST and its capability to handle complex neural network simulations with ease.
Connection concepts in NEST
In the previous post, we learned about the basic concepts of the NEST simulator and how to create a simple single neuron model. This time, we will take a closer look at the connection concepts in NEST, which are crucial for building more complex neural networks.
Step-by-step NEST single neuron simulation
While NEST is designed for large-scale simulations of neural spike networks, the underlying models are based on approximating the behavior of single neurons and synapses. Before using NEST for network simulations, it is probably helpful to first understand the basic functions of the software tool by modelling and studying the behavior of individual neurons. In this tutorial, you will learn about NEST’s concept of nodes and connections, how to set up a neuron model of your choice, how to change model parameters, which different stimulation paradigms are included in NEST and how to record and analyze the simulation results.
NEST simulator – A powerful tool for simulating large-scale spiking neural networks
The NEST simulator is a powerful software tool designed for simulating large-scale networks of spiking neurons (SNN). It has become an essential instrument in the field of computational neuroscience, providing the capability to model, simulate, and analyze the complex dynamics of neuronal systems. And it comes with a user-friendly Python interface, facilitating the construction of neuronal networks with minimal effort.
Simulating spiking neural networks with Izhikevich neurons
The Izhikevich neuron model that we have discussed earlier is known for its simplicity and computational efficiency as well as for its biological plausibility. The model is based on two coupled differential equations that describe the membrane potential and the recovery variable of a neuron. The model can reproduce a wide range of spiking behaviors observed in real neurons, such as regular spiking, fast spiking, chattering, and more. In this post, we explore how we can quickly set up a spiking neural network (SNN) simulation using the Izhikevich neuron model in Python.
Izhikevich model
Computational neuroscience utilizes mathematical models to understand the complex dynamics of neuronal activity. Among various neuron models, the Izhikevich model stands out for its ability to combine biological fidelity with computational efficiency. Developed by Eugene Izhikevich in 2003, this model simulates the spiking and bursting behavior of neurons with a remarkable balance between simplicity and biological relevance. In this post, we explore the properties of the Izhikevich model, examining its application and adaptability in simulating single neuron behaviors.
Hodgkin-Huxley model
An important step beyond simplified neuronal models is the Hodgkin-Huxley model. This model is based on the experimental data of Hodgkin and Huxley, who received the Nobel Prize in 1963 for their groundbreaking work. The model describes the dynamics of the membrane potential of a neuron by incorporating biophysiological properties instead of phenomenological descriptions. It is a cornerstone of computational neuroscience and has been used to study the dynamics of action potentials in neurons and the behavior of neural networks. In this post, we derive the Hodgkin-Huxley model step by step and provide a simple Python implementation.
FitzHugh-Nagumo model
In the previous post, we analyzed the dynamics of Van der Pol oscillator by using phase plane analysis. In this post, we will see, that this oscillator can be considered as a special case of another dynamical system, the FitzHugh-Nagumo model. The FitzHugh-Nagumo model is a simplified model used to describe the dynamics of the action potential in neurons. With a few modifications of the Van der Pol equations we can obtain the model’s ODE system. By again using phase plane analysis, we can then investigate how the dynamics of the system changes under these modifications.
Van der Pol oscillator
In this post, we will apply phase plane analysis to the Van der Pol oscillator. The Van der Pol oscillator is a non-conservative oscillator with nonlinear damping, which was first described by the Dutch electrical engineer Balthasar van der Pol in 1920. We will explore how phase plane analysis can be used to gain insights into the behavior of this system and how it can be used to predict its long-term behavior.
Nullclines and fixed points of the Rössler attractor
After introducing phase plane analysis in the previous post, we will now apply this method to the Rössler attractor presented earlier. We will investigate the system’s nullclines and fixed points, and analyze the attractor’s dynamics in the phase space.
Using phase plane analysis to understand dynamical systems
When it comes to understanding the behavior of dynamical systems, it can quickly become too complex to analyze the system’s behavior directly from its differential equations. In such cases, phase plane analysis can be a powerful tool to gain insights into the system’s behavior. This method allows us to visualize the system’s dynamics in phase portraits, providing a clear and intuitive representation of the system’s behavior. Here, we explore how we can use this method and exemplarily apply it to the simple pendulum.
PyTorch on Apple Silicon
Already some time ago, PyTorch became fully available for Apple Silicon. It’s no longer necessary to install the nightly builds to run PyTorch on the GPU of your Apple Silicon machine as I described in one of my earlier posts.
Rössler attractor
Unlike the Lorenz attractor which emerges from the dynamics of convection rolls, the Rössler attractor does not describe a physical system found in nature. Instead, it is a mathematical construction designed to illustrate and study the behavior of chaotic systems in a simpler, more accessible manner. In this post, we explore how we can quickly simulate this strange attractor using simple Python code.
Understanding Hebbian learning in Hopfield networks
Hopfield networks, a form of recurrent neural network (RNN), serve as a fundamental model for understanding associative memory and pattern recognition in computational neuroscience. Central to the operation of Hopfield networks is the Hebbian learning rule, an idea encapsulated by the maxim ‘neurons that fire together, wire together’. In this post, we explore the mathematical underpinnings of Hebbian learning within Hopfield networks, emphasizing its role in pattern recognition.
Building a neural network from scratch using NumPy
Ever thought about building you own neural network from scratch by simply using NumPy? In this post, we will do exactly that. We will build, from scratch, a simple feedforward neural network and train it on the MNIST dataset.
Python's version logos
Have you ever noticed that Python has introduced individual version logos starting with version 3.10? I couldn’t find any official announcement, but luckily, the Python community on Mastodon was able to help out.
Conditional GANs
I was wondering whether it would be possible to let GANs generate samples conditioned on a specific input type. I wanted the GAN to generate samples of a specific digit, resembling a personal poor man’s mini DALL•E. And indeed, I found a GAN architecture, that allows what I was looking for: Conditional GANs.
Eliminating the middleman: Direct Wasserstein distance computation in WGANs without discriminator
We explore an alternative approach to implementing WGANs. Contrasting from the standard implementation that requires both a generator and discriminator, the method discussed here employs the optimal transport to compute the Wasserstein distance directly between the real and generated data distributions, eliminating the need for a discriminator.
Wasserstein GANs
We apply the Wasserstein distance to Generative Adversarial Networks (GANs) to train them more effectively. We compare a default GAN with a Wasserstein GAN (WGAN) trained on the MNIST dataset and discuss the advantages and disadvantages of both approaches.
Probability distance metrics in machine learning
Probabilistic distance metrics play a crucial role in a broad range of machine learning tasks, including clustering, classification, and information retrieval. The choice of metric is often determined by the specific requirements of the task at hand, with each having unique strengths and characteristics. In this post, we discuss five commonly used metrics: the Wasserstein Distance, the Kullback-Leibler Divergence (KL Divergence), the Jensen-Shannon Divergence (JS Divergence), the Total Variation Distance (TV Distance), and the Bhattacharyya Distance.
Comparing Wasserstein distance, sliced Wasserstein distance, and L2 norm
In machine learning, especially when dealing with probability distributions or deep generative models, different metrics are used to quantify the ‘distance’ between two distributions. Among these, the Wasserstein distance (EMD), sliced Wasserstein distance (SWD), and the L2 norm, play an important role. Here, we compare these metrics and discuss their advantages and disadvantages.
Approximating the Wasserstein distance with cumulative distribution functions
In the previous two posts, we’ve discussed the mathematical details of the Wasserstein distance, exploring its formal definition, its computation through linear programming and the Sinkhorn algorithm. In this post, we take a different approach by approximating the Wasserstein distance with cumulative distribution functions (CDF), providing a more intuitive understanding of the metric.
Wasserstein distance via entropy regularization (Sinkhorn algorithm)
Calculating the Wasserstein distance can be computational costly when using linear programming. The Sinkhorn algorithm provides a computationally efficient method for approximating the Wasserstein distance, making it a practical choice for many applications, especially for large datasets.
Wasserstein distance and optimal transport
The Wasserstein distance, also known as the Earth Mover’s Distance (EMD), provides a robust and insightful approach for comparing probability distributions and finds application in various fields such as machine learning, data science, image processing, and information theory. In this post, we take a look at the optimal transport problem, required to calculate the Wasserstein distance, and how to calculate the distance metric in Python.
Visualizing Occam's Razor through machine learning
Here, we illustrate the concept of Occam’s Razor, a principle advocating for simplicity, by examining its manifestation in the domain of machine learning using Python.
Mamba vs. Conda: Unleashing lightning-fast Python package installations
If you’ve ever experienced the frustration of waiting for ages while installing Python packages with conda, there’s a game-changer I wish I’d heard about earlier: Mamba. This lightning-fast package manager surprised me with its incredible speed, making package installations a breeze. Here is my personal experience and why Mamba is the speed demon you may have been looking for.
Integrate and Fire Model: A simple neuronal model
In this post we explore the Integrate-and-Fire model, a simplified representation of a neuron. We also run some simulations in Python to understand the model dynamics.
Bioimage analysis with Napari
I’ve added new teaching material on using the free and open-source software (FOSS) Napari for bioimage analysis. Feel free to use and share it.
Using random forests for pixel classification
Beyond traditional classification problems, random forests have proven their effectiveness in pixel classification. In this post, we will delve into this domain and explore how random forests can be effectively utilized to tackle the task of pixel classification.
Decision Trees vs. Random Forests for classification and regression: A comparison
Decision trees and random forests are popular machine learning algorithms that are widely used for both classification and regression tasks. In this blog post, we elucidate their theoretical foundations and discuss the differences as well as their advantages and drawbacks.
Image denoising techniques: A comparison of PCA, kernel PCA, autoencoder, and CNN
In this post, we explore the performance of PCA, Kernel PCA, denoising autoencoder, and CNN for image denoising.
Using Autoencoders to reveal hidden structures in high-dimensional data
In this Python tutorial, we explore the application of Autoencoders for dimensionality reduction, demonstrating how this powerful technique can help us uncover and interpret hidden patterns within our data.
Unlocking hidden patterns with Factor Analysis
In this Python tutorial, we dive into Factor Analysis, a powerful statistical method used to uncover hidden, or ‘latent,’ variables within high-dimensional datasets. Like PCA, grasping this technique will allow us to simplify complex data structures, thereby aiding in more effective data interpretation and decision-making.
Untangling complexity: harnessing PCA for data dimensionality reduction
This tutorial explores the use of Principal Component Analysis (PCA), a powerful tool for reducing the complexity of high-dimensional data. By delving into both the theoretical underpinnings and practical Python applications, we illuminate how PCA can reveal hidden structures within data and make it more manageable for analysis.
t-SNE and PCA: Two powerful tools for data exploration
Dimensionality reduction techniques play a vital role in both data exploration and visualization. Among these techniques, t-SNE and PCA are widely used and offer valuable insights into complex datasets. In this blog post, we explore te mathematical background of both methods, compare their methodologies, and discuss their advantages and disadvantages. Additionally, we take a look at their practical implementation in Python and compare the results on different sample datasets.
Understanding L1 and L2 regularization in machine learning
Regularization techniques play a vital role in preventing overfitting and enhancing the generalization capability of machine learning models. Among these techniques, L1 and L2 regularization are widely employed for their effectiveness in controlling model complexity. In this blog post, we explore the concepts of L1 and L2 regularization and provide a practical demonstration in Python.
Understanding gradient descent in machine learning
Gradient descent is a fundamental optimization algorithm widely used in machine learning for finding the optimal parameters of a model. It is a powerful technique that enables models to learn from data by iteratively adjusting their parameters to minimize a cost or loss function. In this blog post, we explore the mathematical background of this method and showcase its implementation in Python.
Loading and saving files in Google Colab
Enable I/O support in your notebooks running in Google Colab with just a few additional commands.
Mutual information and its relationship to information entropy
Mutual information is an essential measure in information theory that quantifies the statistical dependence between two random variables. Given its broad applicability, it has become an invaluable tool in diverse fields like machine learning, neuroscience, signal processing, and more. This post explores the mathematical foundations of mutual information and its relationship to information entropy. We will also demonstrate its implementation in some Python examples.
Information entropy
A fundamental concept that plays a pivotal role in quantifying the uncertainty or randomness of a set of data is the information entropy. Information entropy provides a measure of the average amount of information or surprise contained in a random variable. In this blog post, we explore its mathematical foundations and demonstrate its implementation in some Python examples.
Understanding entropy
In physics, entropy is a fundamental concept that plays a crucial role in understanding the behavior of physical systems. It provides a measure of the disorder or randomness within a system, and its study has far-reaching applications across various branches of physics. This blog post aims to provide a brief overview of entropy in order to gain a better understanding of it.
Zen and natural sciences
In this post, I broaden the scope and explore the intersections of Zen and natural sciences more generally.
The Zen of Python
The connection between Zen and programming is not a subjective one at all. For instance, Python has built it directly into its core programming, known as The Zen of Python.
Bio-image registration with Python
Which method works best for which registration problem? In this tutorial we compare different methods for the registration of bio-images using Python.
How to run PyTorch on the M1 Mac GPU
As for TensorFlow, it takes only a few steps to enable a Mac with M1 chip (Apple silicon) for machine learning tasks in Python with PyTorch.
How to run TensorFlow on the M1 Mac GPU
In just a few steps you can enable a Mac with M1 chip (Apple silicon) for machine learning tasks in Python with TensorFlow.
Is there a difference between miniconda and miniforge?
Simply said: not really. Miniconda is the company driven minimal conda installer, while miniforge is its community driven variant. In the end, you’ll get the same minimal conda installation on your machine – with a minor difference.
Hacks and extensions to improve your coding with Visual Studio Code
This curated list contains useful hacks and extensions to improve the overall coding performance with Visual Studio Code (VS Code).
Setting up Visual Studio Code for Python
In just a few steps you can turn Visual Studio Code (VS Code) into a powerful Python editor for both pure Python code and Jupyter Notebooks.
Enable interactive plots and other plot modes in Jupyter notebooks
Learn how to enable interactive, static and stand-alone window plots in Jupyter notebooks with the magic command
%matplotlib.
Enable code folding in JupyterLab
Learn how to enable code folding in JupyterLab for both, Jupyter Notebooks and pure Python scripts.
How to create and apply a requirements.txt file in Python
Learn how to install Python packages with a requirements.txt file and how to create one yourself.
Virtual environments with venv
In addition to conda’s
create command, Python’s built-in venv command offers another way for creating virtual environments.
Using pip to install Python packages
pip is another package installer for Python. Learn how to use it for installing and managing Python packages in your projects.
How to install and run Python code from GitHub
Learn how to install code from GitHub, that is, e.g., not (yet) available via conda or pip.
A minimal Python installation with miniconda
Learn how to install miniconda to have a quick and minimal Python installation on any operating system. Also learn how to use conda to create and manage virtual environments, install packages, run Python scripts and run Jupyter Notebooks and JupyterLab.
Using Zarr for images – The OME-ZARR standard
As for any other NumPy array, we can use the Zarr file format to store image files. In this post we additionally explore the NGFF (next-generation file format) OME-ZARR standard.
Zarr – or: How to save NumPy arrays
What is Zarr and why is it probably the most suitable file format for saving NumPy arrays?
How to read patch clamp recordings in WaveMetrics IGOR binary files (ibw) in Python
This is a mini tutorial on how to read patch clamp recordings in WaveMetrics IGOR binary files (*.ibw) in Python using the neo and igor packages.
How to add statistical annotations to matplotlib plots
This mini tutorial shows, how to add statistical annotations to matplotlib plots with just a few commands.
Variable Explorer in Jupyter Notebooks
Extend your Jupyter environment with Notebook Extensions and enable, e.g., the option to explore your currently defined variables in a running Jupyter session.
Opening a Jupyter notebook from GitHub in Binder: A step-by-step guide
Opening a Jupyter notebook from GitHub in Binder simplifies access to shared code and facilitates seamless collaboration. With just a few steps, you can launch and interact with Jupyter notebooks directly in your browser, without the need for complex setup procedures.
New Teaching Material: Python Cheat Sheets
I’ve started a collection of various Python cheat sheets that contain some useful and commonly used commands and usage examples.
New Teaching Material: Statistical data analysis and basic time series analysis with Python
I’ve added two new tutorials in the teaching section on statistical data analysis and basic time series analysis with Python.
New Teaching Material: Analyzing IGOR binary files of patch clamp recordings
I’ve added a new tutorial in the teaching section on how to read and process IGOR binary files (ibw) of patch clamp recordings.
strftime Cheat Sheet
Cheat Sheet on formatted date and time strings used, e.g., in Python, C/C++ or even on Jekyll websites by using Liquid tags.
The Weierstrass function and the beauty of fractals
Fractals are captivating mathematical objects that exhibit intricate patterns and self-similarity at various scales. In this post, we explore the elegance and significance of the Weierstrass function, its relation to fractals and fractal geometry, and discuss other notable fractals. Through this journey, we will discover the fascinating world of fractal geometry and its beautiful and profound impact.
The Lotka-Volterra equations: Modeling predator-prey dynamics
The Lotka-Volterra system, also known as the predator-prey equations, is a mathematical model that describes the interaction between two species: predators and their prey. The system captures the dynamic relationship between the population sizes of predators and prey over time, highlighting the intricate balance between them. In this post we explore this system and calculate its numerical solution using numerical integration Python.
Interactive COVID-19 data exploration with Jupyter notebooks
Amidst the ongoing challenges of the COVID-19 pandemic, I have written a Jupyter notebook that facilitates interactive exploration of COVID-19 data. You can select specific countries and visualize key aspects such as confirmed cases, deaths, and vaccinations. The notebook is openly available on GitHub. Feel free to use and share it.
The SIR model: A mathematical approach to epidemic dynamics
In the wake of the COVID-19 pandemic, epidemiological models have garnered significant attention for their ability to provide insights into the spread and control of infectious diseases. One such model is the SIR model, forming the foundation for studying the dynamics of epidemics. In this blog post, we delve into the details of the SIR model, providing a mathematical description, and showcasing its application through a Python simulation.
The two-body problem
The two-body system is a classical problem in physics. It describes the motion of two massive objects that are influenced by their mutual gravitational attraction. The two-body problem is a special case of the n-body problem, which describes the motion of two objects that are influenced by their mutual gravitational attraction. In this post, we make use of Runge-Kutta methods to solve the according equations of motion and simulate the trajectories of artificial satellites around the Earth.
Solving the Lorenz system using Runge-Kutta methods
In my previous post, I introduced the Runge-Kutta methods for numerically solving ordinary differential equations (ODEs), that are challenging to solve analytically. In this post, we apply the Runge-Kutta methods to solve the Lorenz system. The Lorenz system is a set of differential equations known for its chaotic behavior and non-linear dynamics. By utilizing the Runge-Kutta methods, we can effectively simulate and analyze the intricate dynamics of this system.
Runge-Kutta methods for solving ODEs
In physics and computational mathematics, numerical methods for solving ordinary differential equations (ODEs) are of central importance. Among these, the family of Runge-Kutta methods stands out due to its versatility and robustness. In this post we compare the first four orders of the Runge-Kutta methods, namely RK1 (Euler’s method), RK2, RK3, and RK4.
Earth's dipolar magnetic field
In physics and computational mathematics, numerical methods for solving ordinary differential equations (ODEs) are of central importance. Among these, the family of Runge-Kutta methods stands out due to its versatility and robustness. In this post we compare the first four orders of the Runge-Kutta methods, namely RK1 (Euler’s method), RK2, RK3, and RK4.
#Scientific Writing (28)
Exploring connected notes: Local graph views for DEVONthink knowledge bases
DEVONthink has long been my preferred tool for managing personal knowledge. Its smart features, like automatic Wiki-links and AI-based classification, make it ideal for organizing interconnected notes. But these links often stay invisible without a visual layer. To address this, I developed a tool that generates interactive local graphs, embedded directly into each note. These graphs reveal how notes connect, highlighting clusters and patterns that text alone might miss. Fully local and integrated into DEVONthink 3, the system offers a lightweight way to navigate Markdown notes spatially. After refining it for my own workflow, I’m now sharing it for others who might benefit from clearer structure and better insight into their knowledge base.
Bridging ideas on the go: WikiLinks come to DEVONthink To Go
The WikiLinks feature has finally arrived on DEVONthink to go, DEVONthink’s mobile app, which unleashes new possibilities to work with your Personal Knowledge Management (PKM) system on the go.
How to get an RSS feed of your Mastodon bookmarks
The third-party service Mastodon Bookmark RSS allows you to subscribe to your Mastodon bookmarks via RSS, so you don’t forget to make use out of them. You can even integrate the feed into your favorite Zettelkasten apps such as DEVONthink and Obsidian.
Problems with large vaults in Obsidian
In the past few days I played a bit with Obsidian. Turns out that its iOS app has some serious problems with large vaults.
DEVONthink and privacy
One thing I really love about DEVONthink, is its high security and privacy measures regarding the synchronization of my notes across different devices. No other app that I have so far used offered such high standards.
Using VS Code as LaTeX editor
It doesn’t take much to convert Visual Studio Code into a powerful LaTeX editor. Here are the necessary steps that enable full LaTeX support.
The Feynman method as an effective learning tool
The Feynman method can help you not only to remember new knowledge, but also to really and deeply understand it.
How DEVONthink's auto-WikiLink feature changed my Zettelkasten workflow
DEVONthink’s automatic WikiLinks function is a powerful tool, both for discovering connections between notes – expected and unexpected ones – and for the automatized linking of these notes. In this post I briefly explain, how this feature has impacted my Zettelkasten workflow.
DEVONthink Markdown Table-of-Contents generator
I wrote a custom AppleScript for DEVONthink Markdown files, that bypasses the problem of broken links in the auto-generated Table-of-Contents (TOC) of MultiMarkdown (MMD).
Floating Back-to-top button for Markdown documents
You can quickly add a floating Back-to-top button to your Markdown documents in just two steps.
Use your Zettelkasten as a research, thinking and learning tool – Personal knowledge management as a system
In the last part of the series about personal knowledge management, we dive deeper into the Zettelkasten method and demonstrate, how to integrate all parts as an overall system into our research workflow.
Take smart notes with the Zettelkasten method
With the Zettelkasten method by Niklas Luhmann, we give the previously presented personal knowledge network a concrete shape and practical implementation. This is the second of three parts of the series about personal knowledge management.
Don't take isolated notes, connect them! Vannevar Bush on building a self-organizing network of knowledge
In 1945, Vannevar Bush presented his concept of a self-organizing personal knowledge network by linking informational units with each other. This concept, that would later be known as the Hypertext concept or Hypertext theory, provides the theoretical base of the personal knowledge management system presented in the short series on that topic. This is the first of three parts of that series.
Boost your research with a smart personal knowledge management system
My next posts will be a short series about personal knowledge management and how it can be integrated as a holistic system into our overall research workflow. The system is based on the Hypertext Theory and the Zettelkasten method, and its core element is the personal note-taking process. We go step by step through all parts and see, how we can practically implement them into our daily research work.
Clean Thesis: A simple and elegant LaTeX thesis template
If you’re looking for some inspiration for your thesis, I just came across Clean Thesis by Ricardo Langner, a simple and elegant LaTeX template for thesis documents.
New Teaching Material: LaTeX Guide
I’ve added a LaTeX guide to the General Teaching Materials in the teaching section. It serves as a Getting started with LaTeX guide and as a LaTeX glossary.
#Teaching (19)
New teaching material: Functional imaging data analysis – From calcium imaging to network dynamics
We have just completed our new course, Functional Imaging Data Analysis: From Calcium Imaging to Network Dynamics, for the first time as part of the Master of Neuroscience program. This course is now available freely online under ‘Teaching’, alongside my other open educational materials. All resources were created with a strict focus on open content and reproducibility, so that anyone interested can make full use of the lectures, figures, and example code without copyright concerns. Feel free to use and share it.
New teaching material: Dimensionality reduction in neuroscience
We just completed a new two-day course on Dimensionality Reduction in Neuroscience, and I am pleased to announce that the full teaching material is now freely available under a Creative Commons (CC BY 4.0) license. This course is designed to provide an introductory overview of the application of dimensionality reduction techniques for neuroscientists and data scientists alike, focusing on how to handle the increasingly high-dimensional datasets generated by modern neuroscience research.
Assessing animal behavior with machine learning: New DeepLabCut tutorial
I have added a hands-on tutorial to the Assessing Animal Behavior lecture. The tutorial covers the GUI-based use of DeepLabCut, a popular open-source software package for markerless pose estimation of animals. The target group is neuroscience students with no or little programming knowledge. Feel free to share the tutorial with students or colleagues who might be interested in using DeepLabCut for their own projects.
Assessing animal behavior with machine learning
High-throughput and multi-modal behavior experiments, coupled with machine learning analysis, unlock valuable insights into complex systems by capturing diverse behavioral responses and deciphering hidden structures within high-dimensional datasets. I just completed a short introductory lecture on this topic, which is now available in the Teachings section.
Bioimage analysis with Napari
I’ve added new teaching material on using the free and open-source software (FOSS) Napari for bioimage analysis. Feel free to use and share it.
The Feynman method as an effective learning tool
The Feynman method can help you not only to remember new knowledge, but also to really and deeply understand it.
Opening a Jupyter notebook from GitHub in Binder: A step-by-step guide
Opening a Jupyter notebook from GitHub in Binder simplifies access to shared code and facilitates seamless collaboration. With just a few steps, you can launch and interact with Jupyter notebooks directly in your browser, without the need for complex setup procedures.
On teaching
I strongly believe that teaching is not a unidirectional thing, but both sides, the participants and the teacher benefit from it. This is a personal comment on teaching.
New Teaching Material: Python Cheat Sheets
I’ve started a collection of various Python cheat sheets that contain some useful and commonly used commands and usage examples.
New Teaching Material: Statistical data analysis and basic time series analysis with Python
I’ve added two new tutorials in the teaching section on statistical data analysis and basic time series analysis with Python.
New Teaching Material: Analyzing IGOR binary files of patch clamp recordings
I’ve added a new tutorial in the teaching section on how to read and process IGOR binary files (ibw) of patch clamp recordings.
New Teaching Material: Fiji short course
There is a new tutorial in the Teaching Material. It’s a short Fiji tutorial on analyzing biomedical image data.
New Teaching Material: LaTeX Guide
I’ve added a LaTeX guide to the General Teaching Materials in the teaching section. It serves as a Getting started with LaTeX guide and as a LaTeX glossary.
#Web Design (18)
My website is now completely cookie-free
I made several changes to my website to further increase the privacy protection. As a result, it runs now completely without cookies.
Create fancy text styles with Unicode
I found an online font generator to create fancy text styles, simply by using Unicode letters.
On website subscriptions via RSS and Atom feeds
Personal opinion on how to create and maintain personal news feeds beyond the dependence on big social media and tech companies.
Dealing with future posts in Jekyll
While drafting blog posts in Jekyll, you may want to keep some posts hidden from the public eye until they’re ready to be published. In the world of blogging with Jekyll, there are several effective methods to draft such posts without immediately publishing them. Here are three practical approaches.
Running and testing your Jekyll site locally with custom options
Developing with Jekyll often requires running your site locally to test changes before deploying them live. Here is a handy yet useful one-line command that I usually use to run my Jekyll site locally with custom options.
strftime Cheat Sheet
Cheat Sheet on formatted date and time strings used, e.g., in Python, C/C++ or even on Jekyll websites by using Liquid tags.
Liquid Cheat Sheet
This Cheat Sheet gives an overview of Liquid syntax commands one might encounter while developing a Jekyll website.
Minimal Mistakes Cheat Sheet
A quick overview of available commands for creating content with the Minimal Mistakes Jekyll theme.
Running a personal website with Jekyll
I have redesigned my website and moved it to a new host as well: I’m running it as personal Jekyll website hosted on GitHub now.
Restarting my website
In the wake of the COVID-19 pandemic, I have made the decision to relaunch my website. While I have previously utilized my website for smaller personal projects and showcasing my photographs, I now intend to broaden its scope. I will be posting on a range of topics including physics, neuroscience, data science, machine learning, artificial intelligence, open-source projects, and more. As a result, I will be revamping the website in the upcoming months. Stay tuned for the updates.
Posts from 2013 to 2020 moved to the archive
I just cleaned up my website and put a lot of old stuff from 2013 to 2020 into the archive.