Shared dynamics, diverse responses: decoding decision-making in premotor cortex

August 1, 2025 14 minute read see also comments

Last week, I presented a recent study by Genkin et al. (2025), The dynamics and geometry of choice in the premotor cortex, in our Journal Club, and I found it conceptually compelling enough to summarize it here as well. The paper explores how perceptual decisions are encoded not in isolated neural responses but in population-wide latent dynamics. Traditionally, the neuroscience of decision-making has focused on ramping activity in individual neurons, heterogeneous peristimulus time histograms (PSTHs), and decoding strategies based on trial-averaged firing rates. In contrast, this work proposes that a shared low-dimensional decision variable evolves over time and explains the observed diversity in single-neuron responses. In our discussion, we focused on the paper’s central figures, using them to guide a step-by-step reconstruction of the study’s logic and findings.

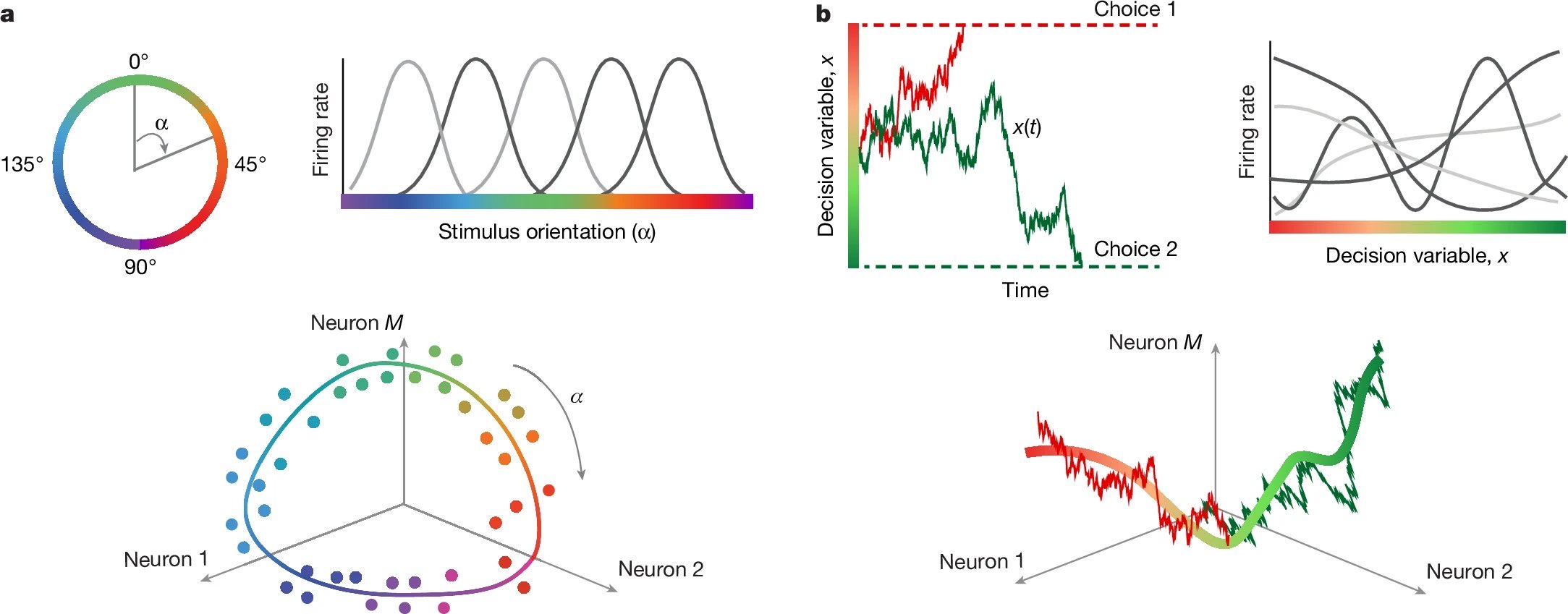
Figure 1: Conceptual framework — neural manifolds for sensory and cognitive variables. a) In sensory cortex, stimulus orientation is encoded via bell-shaped tuning curves, embedding population responses on a circular ring manifold. b) The same principle is hypothesized for cognitive variables: diverse single-neuron tuning to a latent decision variable $x(t)$ gives rise to a low-dimensional decision manifold, along which population activity evolves during single trials. Source: nature.comꜛ (license: CC BY 4.0)

Note: The original article by Genkin et al. (2025)ꜛ and all included figures are distributed under a Creative Commons Attribution 4.0 International License (CC BY 4.0)ꜛ. This means that reuse and redistribution are permitted, including for adaptation and illustration purposes, provided that appropriate credit is given to the original authors and source. All figures shown here are reproduced accordingly under that license.

Conceptual framework

Figure 1 introduces the central idea behind the study: that both sensory and cognitive processes — including decisions — can be represented as trajectories along continuous low-dimensional manifolds in population activity. The discussion begins with a familiar example from sensory neuroscience: neurons in the primary visual cortex encode the orientation of a stimulus, and their population responses, when averaged across trials, form a circular ring structure in the neural state space (Fig. 1a). This serves as a visual metaphor for the broader idea of the paper: that neural activity can be understood as a trajectory along a manifold, where the manifold’s geometry reflects the underlying cognitive process.

Extending this idea, Genkin et al. propose that the internal evolution of a decision can be thought of as movement along a similar one-dimensional trajectory — a “decision manifold” — that unfolds in high-dimensional neural space but is governed by a latent variable shared across the population (Fig. 1b). The goal is to model not just trial-averaged activity, but the actual moment-to-moment population dynamics on single trials as shaped by this latent process.

In contrast, decision-making is typically thought to involve categorical variables. Yet Genkin et al. propose that even decisions can be modeled as trajectories along a smooth, one-dimensional manifold, which they term the “decision manifold”. Rather than analyzing neural activity on a per-neuron basis, they aim to extract a shared latent variable $x(t)$ that captures the internal state of the decision process.

Crucially, each neuron is assumed to have a smooth tuning function $f_i(x)$, which maps the current value of the latent state $x(t)$ to its instantaneous firing rate (Fig. 1c). Neural activity is then explained as the composition of this tuning function with the shared decision trajectory:

\[r_i(t) = f_i(x(t)) + \epsilon\]

where $\epsilon$ represents variability due to spike noise. This means that although observed neural responses are diverse and temporally complex, they are all driven by the same underlying latent process — each neuron simply reads out that process differently.

This insight reframes apparent heterogeneity as structured variation with respect to a shared internal variable. The population as a whole encodes the trajectory $x(t)$, while individual neurons act as non-linear reporters of that latent state. This shift in perspective sets the stage for the generative model and mechanistic analysis that follow.

Task and recordings

To test this framework empirically, Genkin et al. recorded population spiking activity from dorsal premotor cortex (PMd) in macaques trained on a perceptual decision-making task. The task required the animals to discriminate the dominant color (red or green) in a static checkerboard and indicate their decision by reaching to a corresponding target. Task difficulty was systematically manipulated by varying the color coherence — that is, how strongly the stimulus favored one color over the other (Fig. 2a).

Simultaneous multi-electrode recordings in PMd captured the spiking activity of many neurons during this decision process. These data revealed considerable heterogeneity in temporal response profiles across the recorded population: some neurons exhibited clear ramping activity, others responded transiently, and many showed complex patterns depending on the chosen side and stimulus difficulty (Fig. 2b).

This heterogeneity — long considered a hallmark of higher cognitive areas — poses a challenge for standard analysis techniques based on trial-averaged activity. But under the latent manifold hypothesis, such variability can instead be viewed as structured tuning to the same evolving internal decision variable. The observed diversity in firing rates reflects not independent computations, but different nonlinear projections of a shared latent trajectory.

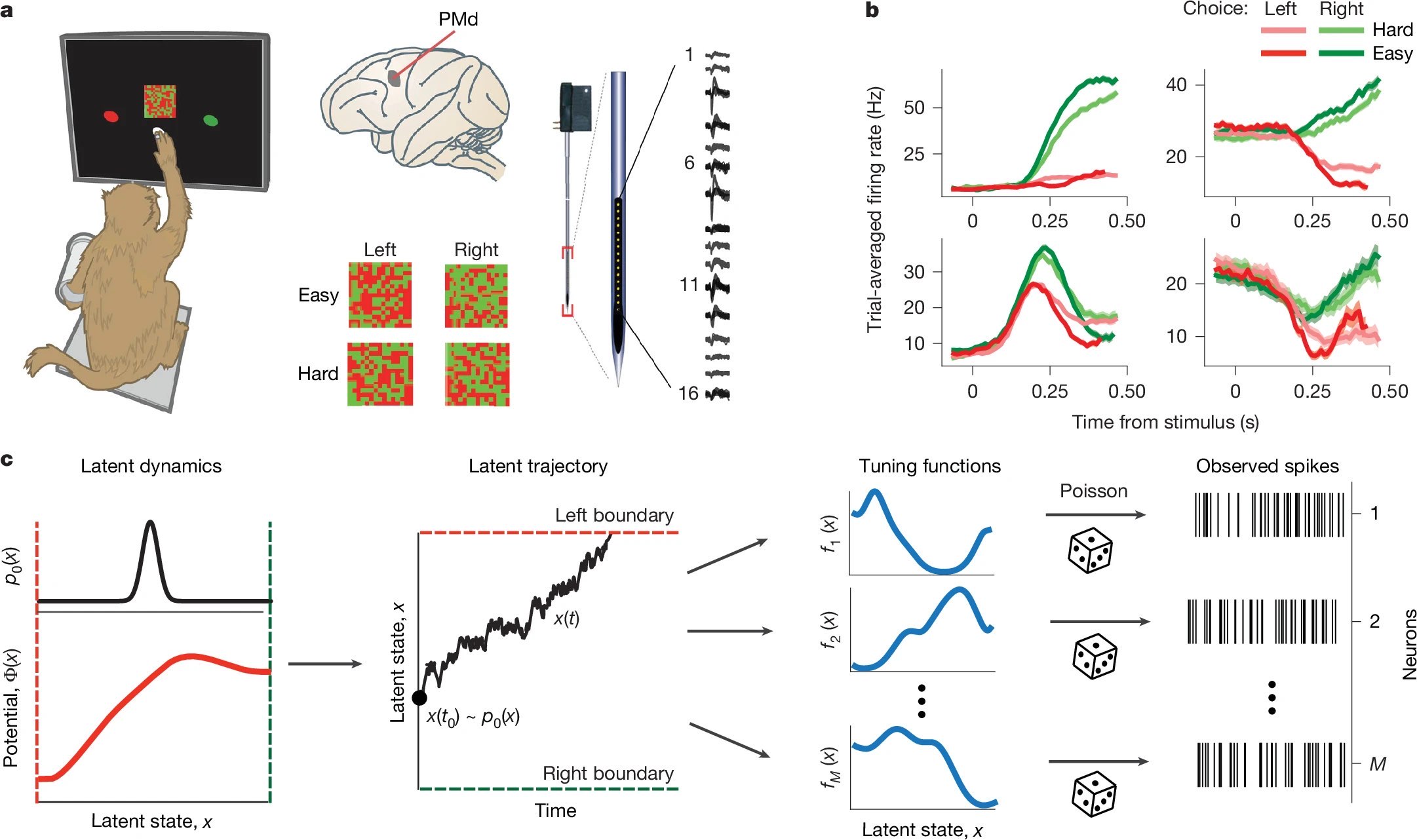
Figure 2: Task, recordings, and generative modeling approach. a) Monkeys performed a color-discrimination task while PMd activity was recorded using multi-electrode arrays. b) Neurons exhibited diverse trial-averaged firing patterns modulated by choice and stimulus difficulty. c) A generative model inferred single-trial latent trajectories $x(t)$, potential functions $\Phi(x)$, and tuning curves $f_i(x)$, linking latent dynamics to observed spikes via Poisson processes. Source: nature.comꜛ (license: CC BY 4.0)

The generative model

With the task and data in place, Genkin et al. constructed a generative model to link the observed spiking activity to latent decision dynamics. The model assumes that every trial is governed by an internal decision variable $x(t)$, which evolves stochastically over time according to a potential function $\Phi(x)$:

\[\frac{dx}{dt} = -D \frac{d\Phi(x)}{dx} + \sqrt{2D}\xi(t)\]

where $\xi(t)$ is Gaussian white noise and $D$ is a diffusion constant controlling stochasticity. The potential $\Phi(x)$ determines the attractor landscape that shapes how the decision variable evolves. Shallow or deep wells correspond to indecision or commitment, respectively.

At the beginning of each trial, $x(0)$ is sampled from an initial distribution $\rho_0(x)$, and the trial terminates when $x(t)$ crosses one of two absorbing decision boundaries. The stochastic evolution of $x(t)$ under the potential thereby determines both the decision outcome and timing.

Each neuron is assigned a smooth tuning function $f_i(x)$, which specifies its instantaneous firing rate as a function of the current latent state. Given $x(t)$ and $f_i(x)$, spike trains are generated via an inhomogeneous Poisson process: $\lambda_i(t) = f_i(x(t))$

The model simultaneously infers the latent trajectories $x(t)$, the potential function $\Phi(x)$, and the tuning curves $f_i(x)$ for all neurons by fitting to the observed spiking activity. This latent-variable framework not only reproduces the diversity of firing patterns but also reveals the internal decision dynamics that give rise to them.

Figure 2c provides a schematic overview of this generative model: a single latent variable $x(t)$ evolves in a stimulus- and noise-dependent potential landscape $\Phi(x)$; its value at any time determines the instantaneous firing rate of each neuron via the tuning curve $f_i(x)$; spike trains are then drawn from a Poisson process based on these rates. The model captures both the geometry and dynamics of population activity on single trials.

Model performance and insight

The model successfully accounts for both trial-averaged activity and trial-to-trial variability in PMd neurons. It performs better than PSTH-based models in explaining spike timing, as indicated by the log-likelihood comparisons across neurons (Fig. 3a). Moreover, the residual variability unexplained by the model correlates closely with expected spike-time variability from Poisson-like processes (Fig. 3b), suggesting that the model approaches the limit of what is explainable from spike data.

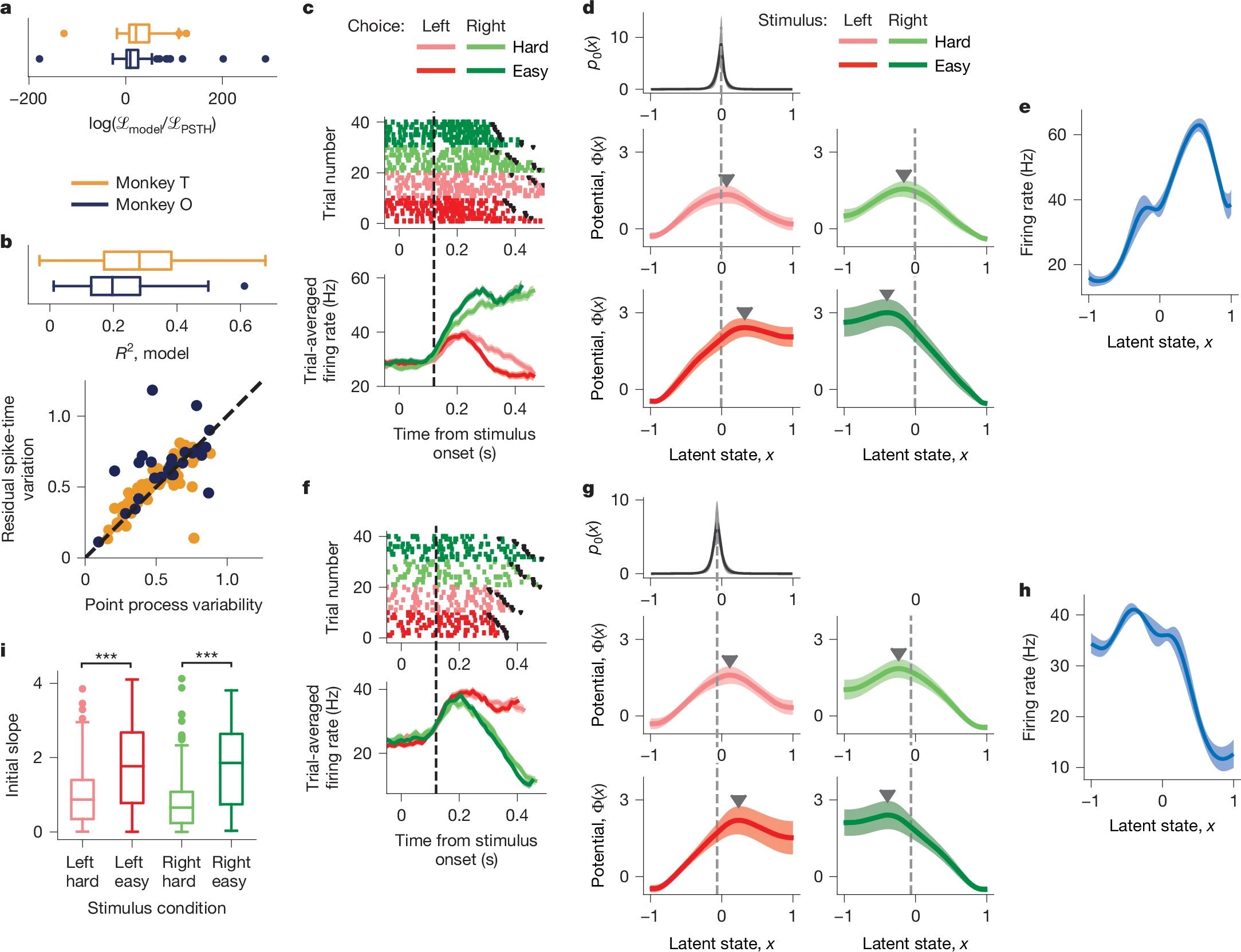
Figure 3: Single-neuron decision dynamics and model validation. a–b) The single-neuron model outperforms PSTH fits in likelihood and explains spike-time variability. c–e) For one neuron, the model captures trial-wise spiking, infers a potential with a single barrier, and recovers a smooth tuning function. f–h) Same for a second neuron. i) Across neurons, easier trials correspond to steeper potential slopes at initial states, indicating faster dynamics. Source: nature.comꜛ (license: CC BY 4.0)

To illustrate how the model captures single-neuron activity, Fig. 3c–e shows data from an example neuron. Its raster plot and PSTH reveal clear modulations by stimulus difficulty and choice direction. Despite these variations, the same smooth tuning function $f_i(x)$ explains the neuron’s response across all conditions (Fig. 3e). Differences between conditions are instead captured by changes in the potential $\Phi(x)$, which governs the speed and direction of the latent state $x(t)$ (Fig. 3d). The initial state distribution $p_0(x)$ for this neuron tends to peak near the shallow slope of the potential, from which the decision trajectory begins.

Another neuron (Fig. 3f–h) exhibits a different tuning function and potential landscape, again illustrating the diversity of encodings for a shared latent process. Yet the model maintains a consistent structure: each neuron encodes $x(t)$ through its own $f_i(x)$, while task conditions modulate $\Phi(x)$.

Finally, Fig. 3i summarizes a key result: trials with easier stimuli induce steeper potential slopes near $p_0(x)$, effectively accelerating the decision trajectory. This provides a mechanistic account of shorter reaction times on easy trials, not due to stronger inputs but due to sharper internal dynamics.

These findings highlight the central promise of the framework: diverse and variable spiking patterns can be interpreted as manifestations of a smooth, low-dimensional, task-modulated latent dynamic — shared across the population.

Population-level decoding and validation

A core strength of the modeling approach is its ability to leverage shared population-level dynamics for decoding. Genkin et al. compare the performance of their population model against simpler alternatives — namely, single-neuron models and logistic regression on raw spiking data. Using leave-one-neuron-out cross-validation and behavioral prediction metrics, they show that the population-based latent-variable model consistently outperforms all baselines in terms of spike train likelihood and behavioral decoding accuracy (Fig. 4a,e).

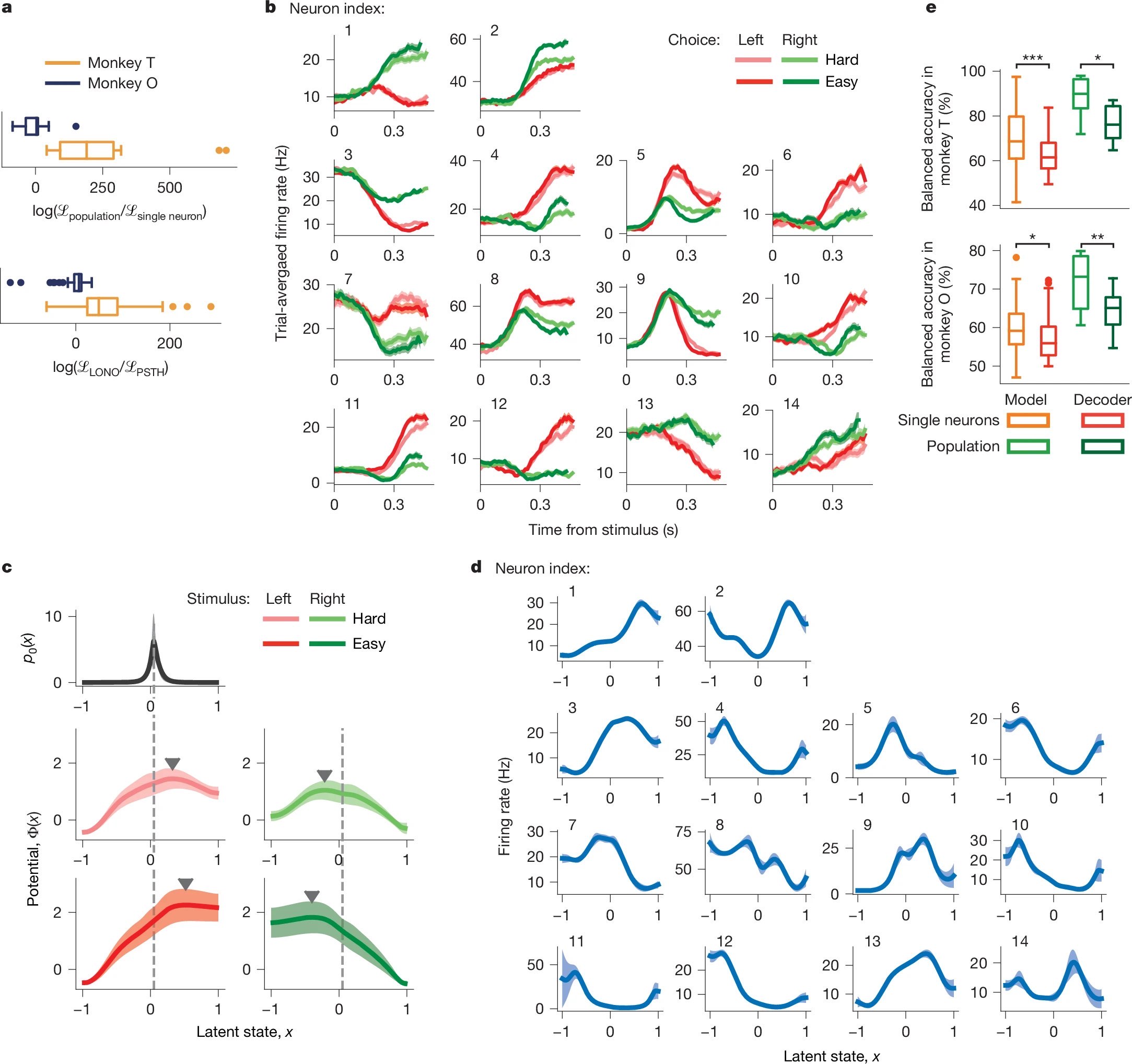
Figure 4: Population-level modeling improves fit and behavioral prediction. a) Population models outperform single-neuron models in likelihood and cross-validation. b) Simultaneously recorded neurons show diverse firing across conditions. c–d) Inferred population potentials and tuning functions reveal shared latent dynamics. e) Population models yield higher choice-prediction accuracy than single-neuron models or decoders. Source: nature.comꜛ (license: CC BY 4.0)

Crucially, the model allows for disentangling the structured tuning of individual neurons from the time-varying latent trajectory $x(t)$, which varies with task condition and trial difficulty. As shown in Fig. 4d, each neuron maintains a fixed, smooth tuning function $f_i(x)$ across conditions, while Fig. 4c illustrates how the changing latent trajectory $x(t)$, shaped by $\Phi(x)$, accounts for variability in observed responses. Differences in observed neural responses (Fig. 4b) thus emerge from the changing latent trajectories $x(t)$, not from dynamic remapping of the tuning functions.

This separation provides a powerful insight: the apparent heterogeneity in trial-averaged PSTHs reflects diverse yet fixed encodings of a shared dynamic variable. The resulting population decoding strategy, grounded in latent dynamics, offers more robust behavioral prediction than traditional neural representations.

In short, latent dynamics — not individual spikes — carry the core signal. And when captured at the population level, they enable both accurate modeling of single-neuron activity and high-fidelity decoding of behavior.

Mechanistic models

The final part of the paper investigates the circuit-level plausibility of the observed latent dynamics by simulating two types of recurrent neural network models. Both are constrained to be low-dimensional, and both are evaluated by their ability to reproduce the empirical tuning functions $f_i(x)$, potential landscapes $\Phi(x)$, and the decision trajectories $x(t)$.

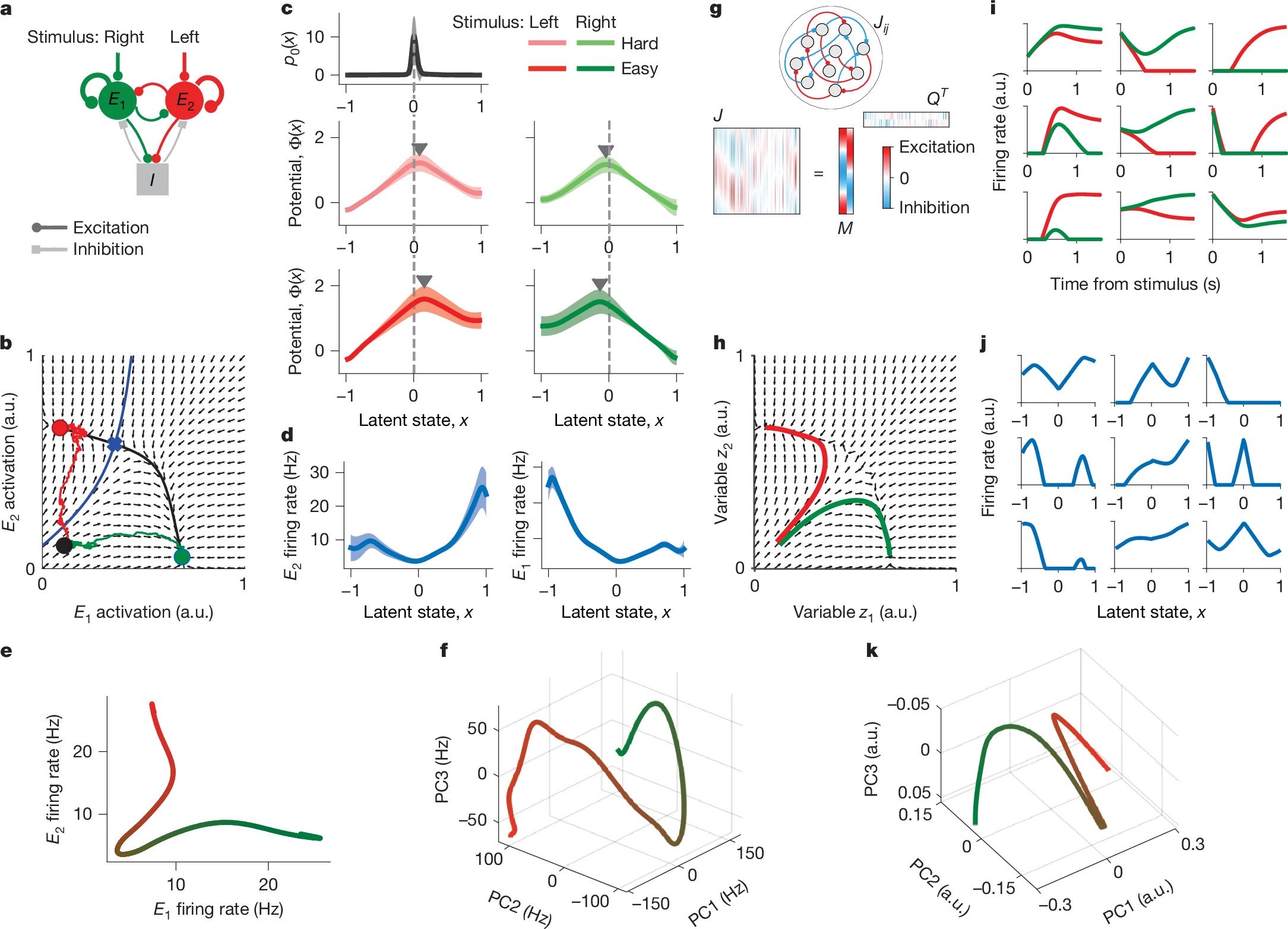
Figure 5: Recurrent network models reproduce latent dynamics and decision geometry. a) A minimal spiking network with two excitatory populations (E1 and E2) and one inhibitory population (I) implements winner-take-all dynamics. b) Its mean-field dynamics form a 2D phase space with two stable attractors separated by a saddle and a separatrix. c–d) Fitting the model-generated spikes with the latent variable framework recovers decision potentials and tuning functions similar to those inferred from real PMd data. e) The model defines a compact decision manifold via its tuning functions. f) By contrast, PMd data exhibit a more complex decision manifold when tuning functions are projected into principal component space. g–h) A low-rank RNN with structured connectivity replicates the attractor dynamics in a higher-dimensional latent space. i–k) This RNN generates choice-selective activity and tuning curves that map onto a realistic, low-dimensional decision manifold. Source: nature.comꜛ (license: CC BY 4.0)

First, Genkin et al. implement a minimal mutual-inhibition model with three neural populations (Fig. 5a): one representing leftward decisions, one representing rightward decisions, and a shared inhibitory pool that mediates mutual suppression between the decision groups. This model naturally produces bistable attractor dynamics, where the system converges to one of two states depending on small fluctuations in the initial condition. This bistability — a classical mechanism for decision-making — yields potential functions $\Phi(x)$ with a central barrier separating two wells (Fig. 5c), mirroring the structure inferred from data.

The resulting latent dynamics (Fig. 5b) show stable flow fields toward either decision basin. The corresponding tuning functions for the decision units $E_1$ and $E_2$ are smooth and selective for different ranges of the latent variable (Fig. 5d). The resulting decision manifold, when plotted as $E_1$ versus $E_2$ firing rate, is a simple curve separating the decision states (Fig. 5e).

To assess whether such a simple geometry suffices to explain empirical data, the authors compare it to the decision manifold extracted from real PMd activity. Specifically, they project the tuning functions of all PMd neurons onto the first three principal components, revealing a more intricate 3D trajectory (Fig. 5f). This suggests that while the mutual-inhibition model captures the basic structure of decision dynamics, it lacks the representational richness seen in real population activity.

To bridge this gap, Genkin et al. simulate a more flexible, high-dimensional recurrent neural network (RNN) with low-rank connectivity (Fig. 5g). The network is initialized with random connections constrained to a low-rank form $J = M Q^T$, where $M$ and $Q$ define the effective dynamics. Despite this architectural simplicity, the RNN gives rise to structured, low-dimensional trajectories (Fig. 5h) and trial-averaged responses that resemble those of real PMd neurons (Fig. 5i). Tuning functions extracted from this network again display heterogeneous yet coherent mappings from the latent variable $x$ to firing rate (Fig. 5j).

Moreover, the decision manifold of the RNN model (Fig. 5k) approximates the curved structure of the empirical PMd manifold (Fig. 5f) more closely than the minimal mutual-inhibition model did (Fig. 5e). This shows that more realistic population dynamics — including geometry, stability, and tuning diversity — can emerge from structured but generic recurrent architectures, even without specific optimization for the task.

Together, these mechanistic models demonstrate that latent decision dynamics — including the emergence of shared potential landscapes and diverse tuning — can naturally arise from generic recurrent circuit motifs, with or without task-specific training.

Interpretation and limitations

Genkin et al. provide a deeply insightful and elegant demonstration of how decision dynamics in premotor cortex can be reconstructed from single-trial data using a low-dimensional generative model. By inferring latent trajectories $x(t)$, tuning functions $f_i(x)$, and potential landscapes $\Phi(x)$, they show that complex decision behavior can be explained through structured but low-dimensional neural dynamics. Their framework bridges neural population activity, behavioral choices, and dynamical systems theory, providing a rich and unified perspective on cortical computation during decision-making.

Nevertheless, some important conceptual distinctions and limitations should be acknowledged. The entire modeling approach is retrospective: it infers the structure of decision dynamics from already trained monkeys performing a familiar task. As such, it explains how decisions are executed, not how the underlying representations — including potentials and tuning curves — are acquired.

This limitation becomes particularly relevant when considering the mechanistic RNN models in Fig. 5. While these networks reproduce the qualitative structure of the latent dynamics, they are not trained on empirical PMd spiking activity, nor do they implement biologically plausible learning mechanisms. Their dynamics emerge from architectural constraints (e.g., mutual inhibition or low-rank connectivity), but not from plasticity or experience-dependent adaptation.

Ultimately, to fully understand cortical decision-making, future work will need to connect these elegant reconstructions to models of learning and plasticity — that is, to show how realistic neural circuits can develop the very potential landscapes and low-dimensional trajectories that Genkin et al. so convincingly describe.

Take-home messages and conclusion

To sum this up, the study by Genkin et al. (2025)ꜛ offers a new perspective on how internal cognitive variables — such as decisions — can be decoded and interpreted from population activity:

Population activity encodes decisions via shared internal dynamics.
Neuronal heterogeneity corresponds to structured tuning to a common latent state.
Recurrent connectivity provides a plausible mechanistic substrate for these dynamics.

I chose this paper for our Journal Club because it elegantly combines data analysis, theory, and modeling to bridge the gap between individual spiking activity and population-level decision dynamics. I particularly appreciate how it brings conceptual clarity to the nature of neural variability — showing that it can reflect structured responses to shared latent variables, rather than just noise. And beyond the results themselves, the authors have made their model publicly available as a Python package called NeuralFlowꜛ, allowing anyone interested to explore and test the framework further. That makes this not only a powerful but also an accessible contribution to computational neuroscience in my view.

References and useful links

Mikhail Genkin, Krishna V. Shenoy, Chandramouli Chandrasekaran & Tatiana A. Engel, The dynamics and geometry of choice in the premotor cortex, 2025, Nature, doi: 10.1038/s41586-025-09199-1
NeuralFlowꜛ on GitHub