On the role of gap junctions in neural modelling

7 minute read see also comments

↑

Gap junctions are specialized intercellular connections that facilitate direct electrical and chemical communication between neurons. Unlike synaptic transmission, which involves neurotransmitters, gap junctions enable the direct passage of ions and small molecules through channels formed by connexins (a family of transmembrane proteins that assemble to create gap junction channels), leading to synchronized neuronal activity. In computational neuroscience, modeling gap junctions is crucial for understanding their role in neural network dynamics, synchronization, and various brain functions.

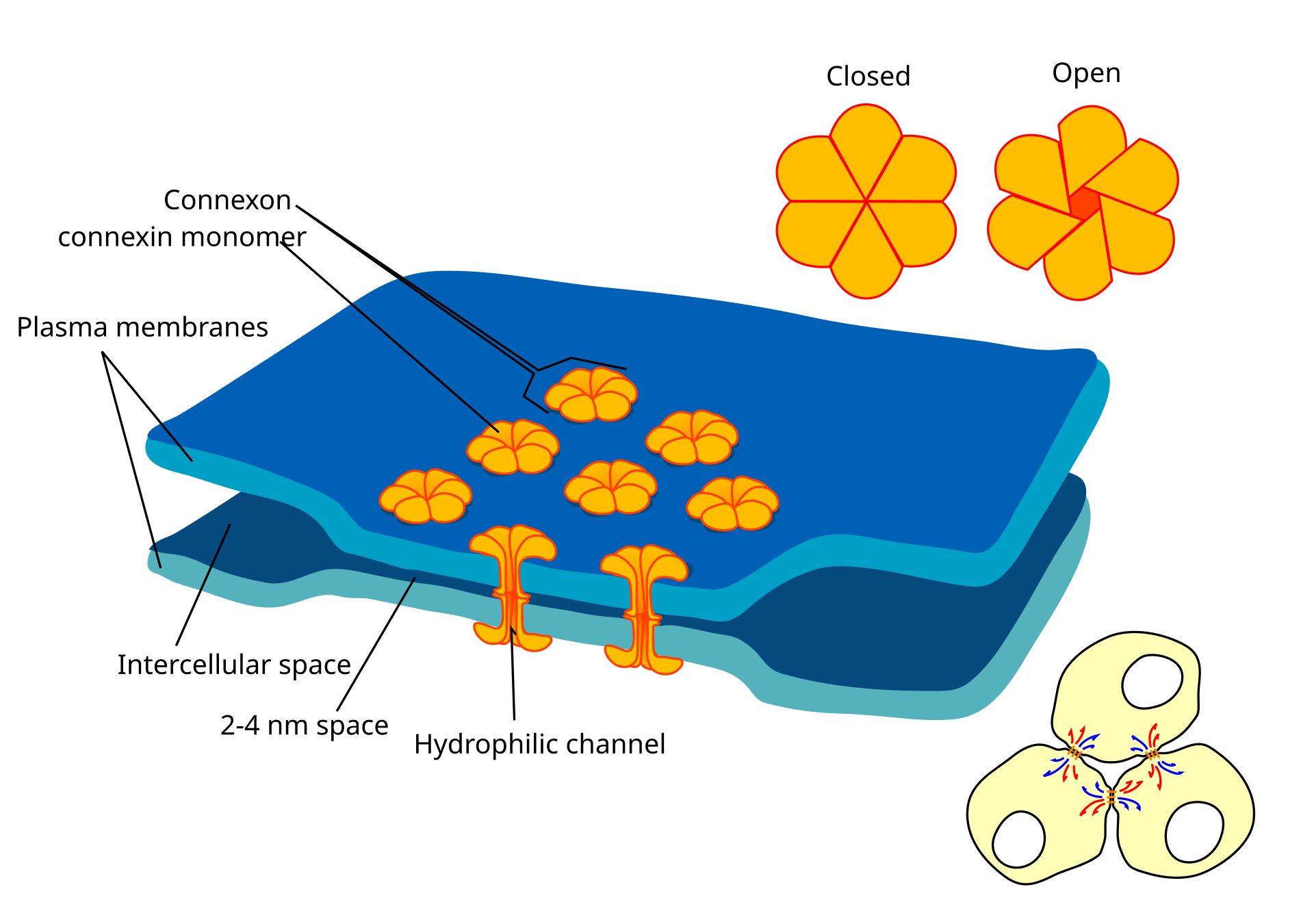Connexon pairing across membranes bridges the gap between two cells and between vesicles to membranes. Schematic representation of gap junctions between two cells. Shown are patches of cell membranes (blue) of two cells, which are connected by connexons (orange). The connexons are formed by six connexin proteins each. The connexons of the two cells align and form a continuous hydrophilic channel between the cells, bridging the intercellulare space, and are able to close and open. In the lower right corner, three exemplary cells are shown, which are connected by gap junctions. Source: Wikimedia Commonsꜛ (license: CC BY-SA 4.0)

Biological explanation and relevance

Gap junctions consist of a specific type of intercellular channel formed by so-called connexin proteins, which form a connexon. Each connexon from one neuron aligns with a connexon from an adjacent neuron, creating a continuous aqueous pathway that allows ions and small molecules to pass directly between cells. The distance between neurons connected by gap junctions can be as small as 2 nm, allowing for near-instantaneous signal transmission. The channels of the gap junction are formed from two half-channels (connexons), of which each cell contributes one.

Gap junctions facilitate communication between neighboring cells. Ions or small molecules are transferred directly from one cell to the neighboring cell through diffusion. These can be potassium or calcium ions serving as signal transmitters, secondary messengers such as cAMP, cGMP, or IP3, or small metabolic products like glucose. The selectivity of the transition depends on the specific structure of the cell channel and can be controlled by signaling mechanisms such as the membrane potential. Some types of channels also selectively transport certain substances in only one direction.

Beyond neurons, astrocytes form extensive gap-junction networks primarily via Cx43/Cx30, supporting $[K^{+}]$ buffering, metabolic coupling, and tissue-scale $[Ca^{2+}]$ waves—broadening the relevance of gap junctions for brain physiology.

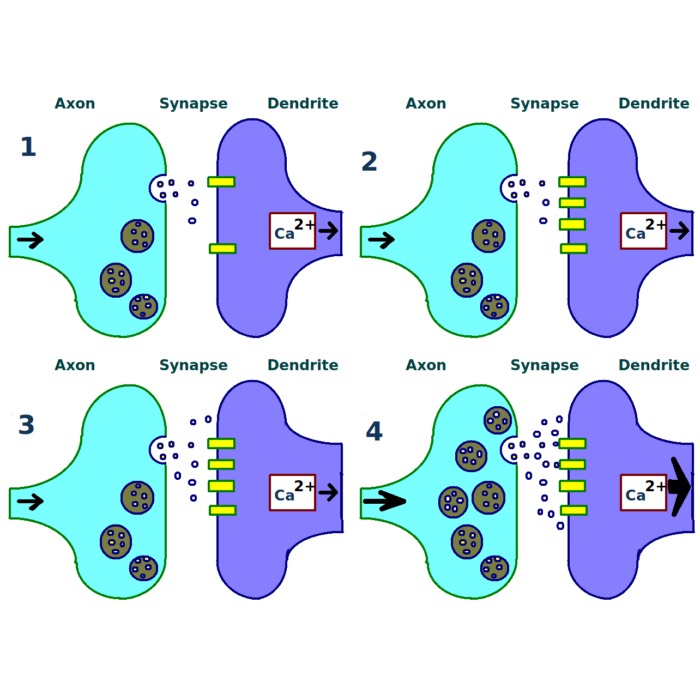
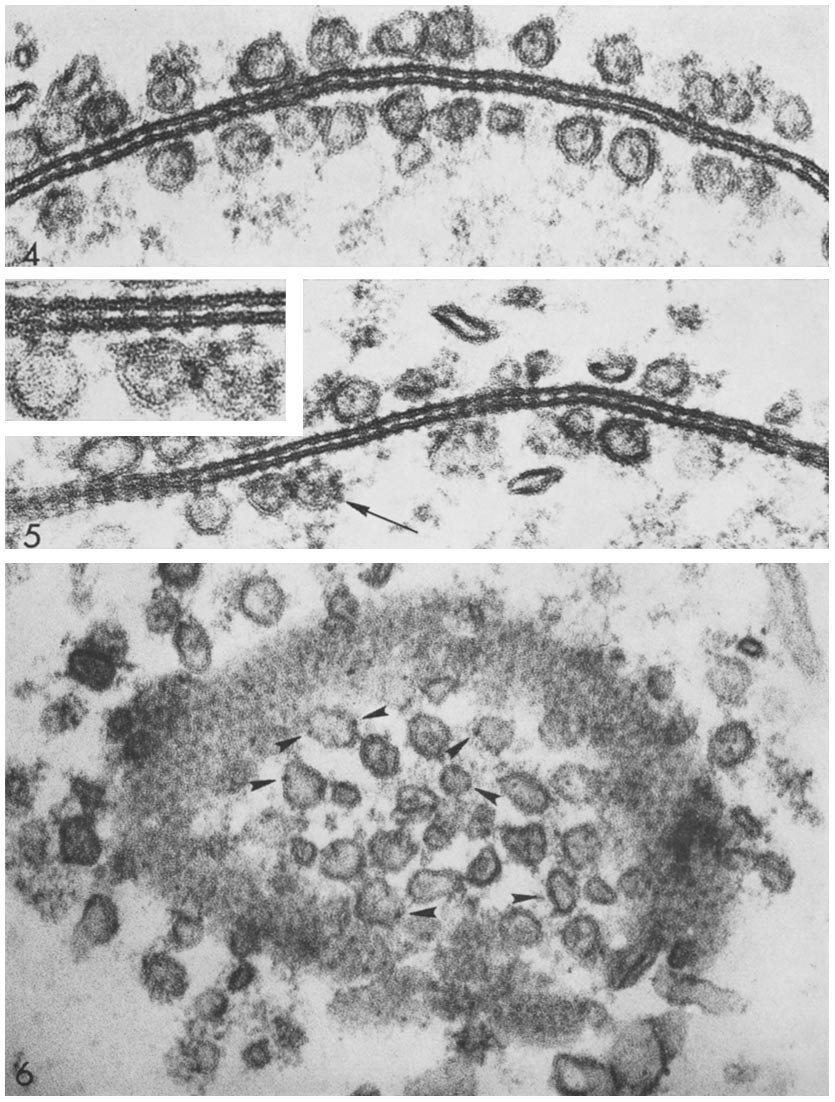Connexon pairing across membranes bridges the gap between two cells and between vesicles to membranes. Connexon pairing across membranes bridges the gap between two cells and between vesicles to membranes. Source: Wikimedia Commonsꜛ (license: CC BY-SA 4.0)

Key functions of gap junctions are:

  1. Synchronization: Gap junctions synchronize the electrical activity of coupled neurons, which is essential for processes like rhythmic oscillations and coordinated muscle contractions.
  2. Development and plasticity: They play a role in the development of neural circuits and can influence synaptic plasticity.
  3. Signal propagation: Gap junctions facilitate the propagation of electrical signals across networks of neurons, which can be critical in areas such as the retina and certain brain regions.

Gap junctions as electrical synapses

Gap junctions located in neurons are often referred to as electrical synapses due to their ability to transmit electrical signals directly between cells. They function as voltage-controlled, transmitter-free synapses in neurons, but also in the retina and the heart. They enable rapid and synchronous propagation of action potentials. The conductivity of gap junctions varies with the composition of different connexins. They are not as numerous in neurons as chemical synapses, but they have also been found in glial cells, whose involvement in neuronal events beyond supplying the nerve cells is currently being investigated. The main task of electrical synapses appears to be the synchronization of groups of nerve cells that serve as oscillators and rhythm generators.

How do electrical synapses work?

The depolarization of the presynaptic cell leads to a potential gradient between the two cells connected by gap junctions, allowing cations to flow from the presynaptic cell towards the postsynaptic cell and anions to flow from the post- to the presynaptic cell. If the threshold value at the postsynaptic membrane is exceeded, an action potential follows, and the signal can be transmitted with practically no time delay (10-5 s), enabling the synchronization of many cells, such as in the heart muscle, due to the small time delay.

Comparison between electrical and chemical synapse

In addition to the much shorter time delay, electrical synapses differ from chemical synapses in that the transmission of excitation can usually take place in both directions. Gap junctions of some cells can also be regulated in their current direction, either dependent on $[Ca^{2+}]$ or dependent on membrane potential. However, gap junctions as transmitters of excitation also have some disadvantages: direct transmission of excitation to distant cells is not possible, and excitation cannot be used to inhibit another cell.

Some electrical synapses are rectifying (direction-biased) and dynamically gated; this makes their effective coupling state context-dependent in ways not captured by purely ohmic intuition.

Importance in neural networks

In neural networks, gap junctions contribute to the generation and maintenance of oscillatory activity, which is important for functions like memory consolidation and sensory processing. They also play a role in the spread of epileptic activity and the synchronization of neuronal firing patterns.

Mathematical modeling of gap junctions

In computational models, gap junctions are typically represented by adding a conductance term to the differential equations governing the membrane potentials of coupled neurons. The conductance of a gap junction ($g_{gap}$) is analogous to a resistor in an electrical circuit.

For two neurons $i$ and $j$ with membrane potentials $V_i$ and $V_j$, the current ($I_{gap}$) flowing through the gap junction can be described by:

\[I_{gap} = g_{gap} \cdot (V_i - V_j)\]

where:

  • $g_{gap}$ is the conductance of the gap junction.
  • $V_i$ and $V_j$ are the membrane potentials of the neurons.

The differential equation for the membrane potential $V_i$ of neuron $i$ incorporating the gap junction current can be written as:

\[C_m \frac{dV_i}{dt} = -I_{ion}(V_i) + I_{ext} + \sum_j I_{gap}\]

where:

  • $C_m$ is the membrane capacitance,
  • $I_{ion}(V_i)$ is the ionic current,
  • $I_{ext}$ is the external input current, and
  • $\sum_j I_{gap}$ is the sum of currents from all neurons $j$ connected to neuron $i$ via gap junctions.

Modeling gap junctions with NEST Simulator

Below is a Python example using the NEST simulator. We model two neurons with Hodgkin-Huxley dynamics connected by a gap junction and simulate their membrane potentials. We use NEST’s hh_psc_alpha_gap neuron model, which includes gap junctions. The code is adapted and slightly modified from the NEST tutorial tutorial “Gap Junctions: Two neuron example”ꜛ.

import matplotlib.pyplot as plt
import numpy as np
import nest

# set global properties for all plots:
plt.rcParams.update({'font.size': 12})
plt.rcParams["axes.spines.top"]    = False
plt.rcParams["axes.spines.bottom"] = False
plt.rcParams["axes.spines.left"]   = False
plt.rcParams["axes.spines.right"]  = False

nest.set_verbosity("M_WARNING")
nest.ResetKernel()

# set the simulation resolution and time:
nest.resolution = 0.05 # ms
T = 350.0 # ms

# create two neurons with Hodgkin-Huxley dynamics and gap junctions:
neuron = nest.Create("hh_psc_alpha_gap", 2)

# set the parameters of the neurons:
neuron.I_e    = 100.0 # constant external input current [pA]
neuron[0].V_m = -10.0 # initial membrane potential of neuron 1 [mV]

# create a voltmeter to record the membrane potential:
voltmeter = nest.Create("voltmeter", params={"interval": 0.1})

# connect the voltmeter to the neurons:
nest.Connect(voltmeter, neuron, "all_to_all")

# connect the neurons with gap junctions:
nest.Connect(
    neuron, neuron, 
    {"rule": "all_to_all", "allow_autapses": False}, 
    {"synapse_model": "gap_junction", "weight": 0.5})

# simulate the network:
nest.Simulate(T)

# extract the data from the voltmeter:
senders = voltmeter.events["senders"]
times = voltmeter.events["times"]
v_m_values = voltmeter.events["V_m"]

# plots:
plt.figure(figsize=(6, 4))
plt.plot(times[np.where(senders == 1)], v_m_values[np.where(senders == 1)], label="neuron 1")
plt.plot(times[np.where(senders == 2)], v_m_values[np.where(senders == 2)], label="neuron 2")
plt.xlabel("time [ms]")
plt.ylabel("membrane potential [mV]")
plt.title("Membrane potential of two HH neurons\nwith gap junctions")
plt.legend()
plt.tight_layout()
plt.show()

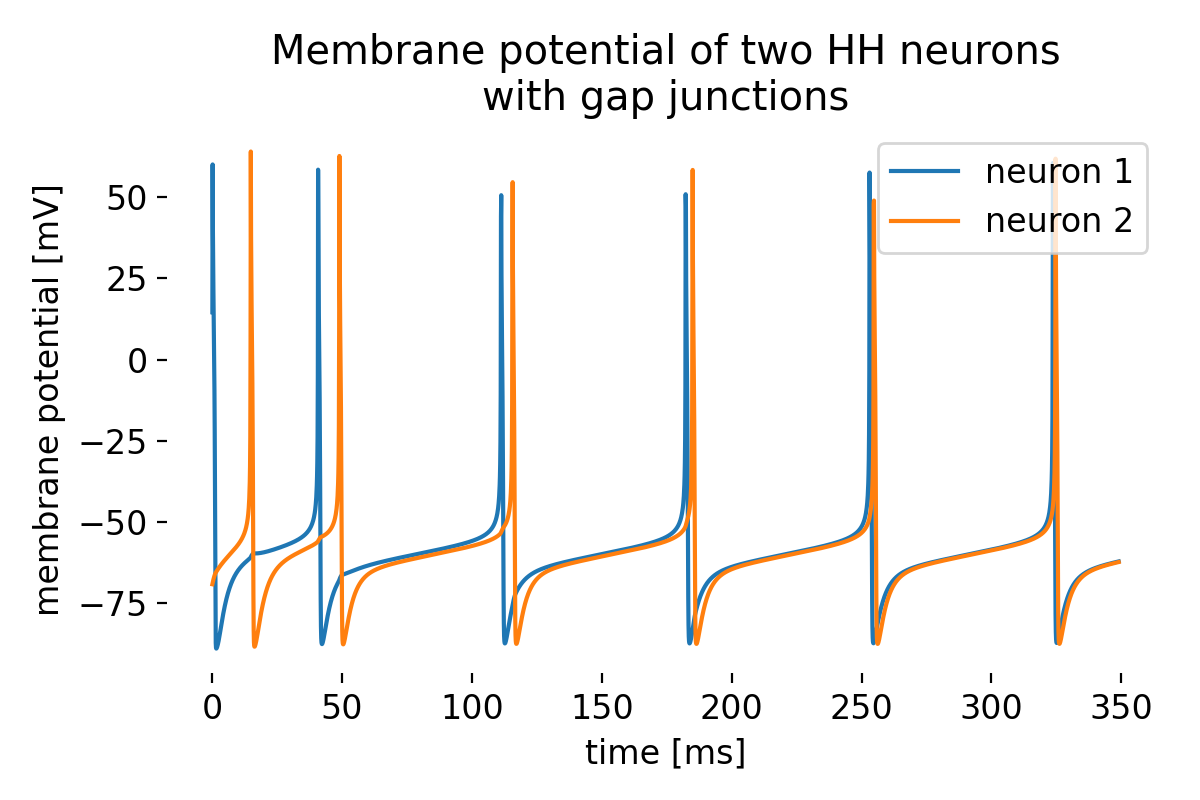TEXT. Membrane potential of two Hodgkin-Huxley neurons connected by a gap junction. The neurons exhibit synchronized activity due to the gap junction.

While being asynchronous at the beginning, the neurons quickly synchronize their activity due to the gap junction. This short example demonstrates how gap junctions can influence the dynamics of a neural network and lead to synchronized behavior.

Conclusion

Gap junctions play a critical role in neural communication and synchronization. Modeling these connections computationally provides valuable insights into their function and impact on neural network dynamics. The mathematical framework and example code presented here illustrate how gap junctions can be incorporated into computational models to study their effects on neuronal behavior and network function.

The complete code used in this blog post is available in this Github repositoryꜛ (two_neurons_with_gap_junctions.py). Feel free to modify and expand upon it, and share your insights.

References

2 other articles are linked to this site

Related posts

Bienenstock-Cooper-Munro (BCM) rule

15 minute read

The Bienenstock-Cooper-Munro (BCM) rule is a cornerstone in theoretical neuroscience, offering a comprehensive framework f...

comments