Blog
Articles about computational science and data science, neuroscience, and open source solutions. Personal stories are filed under Weekend Stories. Browse all topics here. All posts are CC BY-NC-SA licensed unless otherwise stated. Feel free to share, remix, and adapt the content as long as you give appropriate credit and distribute your contributions under the same license.
tags · RSS · Mastodon · simple view · page 17/19
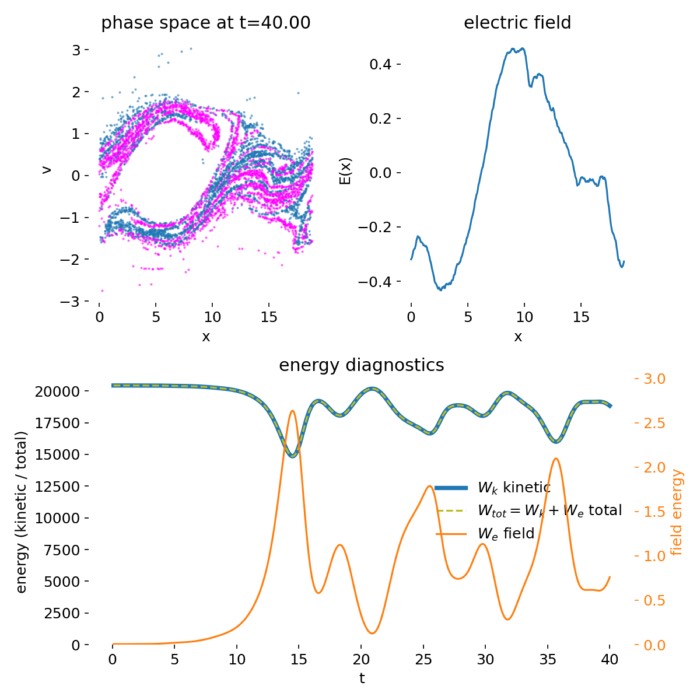
A spectral (FFT) Poisson solver for 1D electrostatic PIC
In our previous post on Particle-in-Cell methods, we implemented a minimal 1D electrostatic PIC code using a finite difference Poisson solver. Here, we present an alternative implementation that uses a spectral Poisson solver based on FFTs, highlighting the differences and advantages of this approach.
Particle-in-Cell methods in kinetic plasma simulations
The Particle-in-Cell (PIC) method is a powerful numerical technique for simulating kinetic plasmas by combining particle dynamics with grid-based field solvers. In this post, we explore the fundamental principles of PIC, its mathematical formulation, and its applications in space plasma physics.
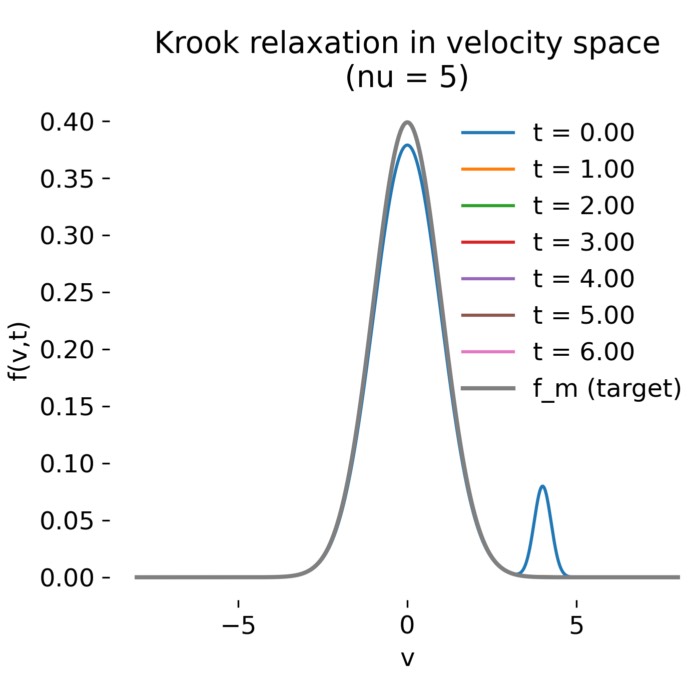
Krook collision operator as velocity-space relaxation
The Krook collision operator provides a minimal model for velocity-space relaxation in kinetic plasma theory. In this post, we explore its properties and physical interpretation.
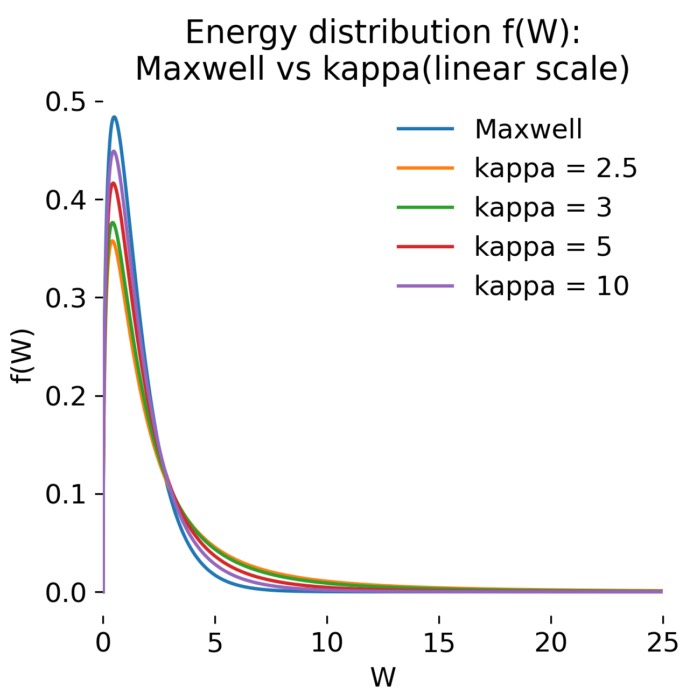
Kappa versus Maxwell distributions: Suprathermal tails in collisionless plasmas
In many space plasmas, particle velocity distributions deviate from the Maxwellian form due to weak collisionality. Kappa distributions, characterized by suprathermal tails, provide a more accurate description of these environments. In this post, we compare Maxwellian and kappa energy distributions, highlighting the emergence of suprathermal populations and their significance in space plasma physics.
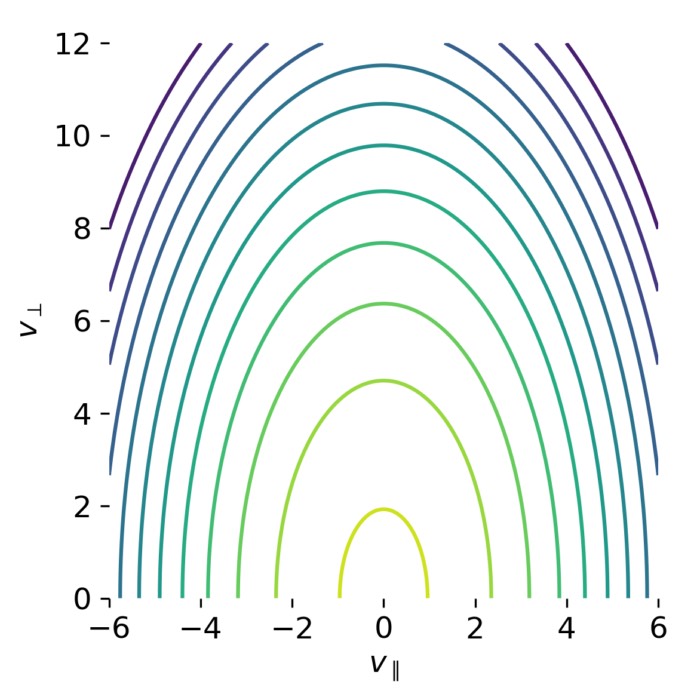
Bi-Maxwellian distributions and anisotropic pressure
In many space and laboratory plasmas, velocity distributions are anisotropic with respect to the magnetic field direction. This leads to anisotropic pressure components that cannot be captured by fluid models assuming a scalar pressure. In this post, we construct bi-Maxwellian velocity distributions with prescribed temperature anisotropies and demonstrate explicitly how they give rise to anisotropic pressure tensors. The numerical results reproduce known analytic relations while providing an intuitive geometric interpretation in velocity space.
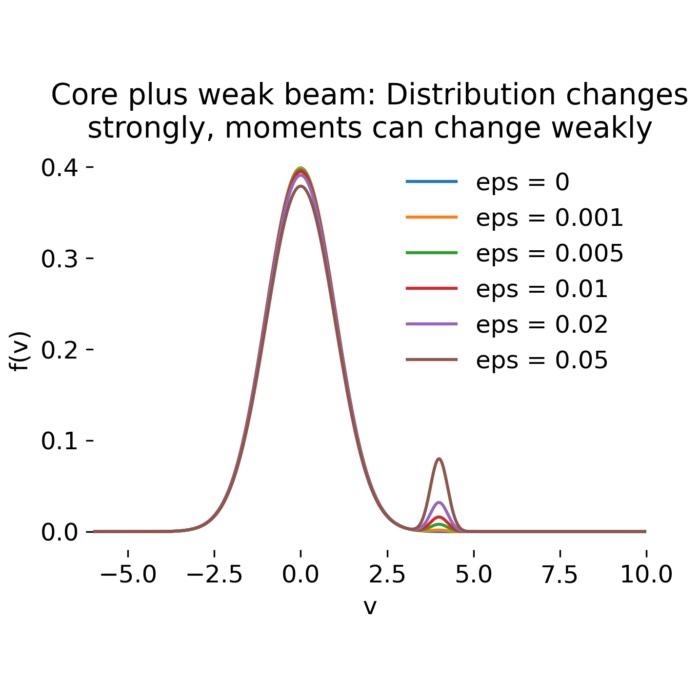
What velocity moments miss: Core plus beam distributions
In this post, we explore how different initial velocity distributions lead to qualitatively distinct macroscopic dynamics, illustrating the inherently kinetic nature of these processes.
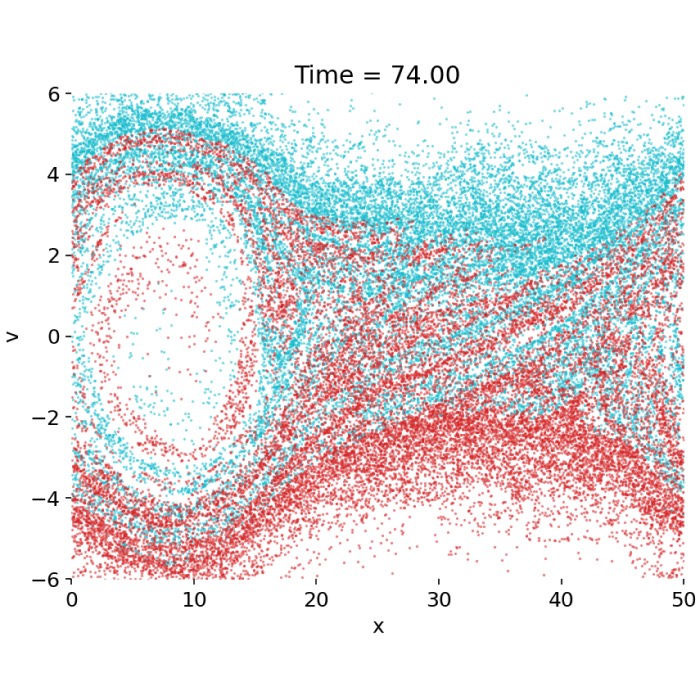
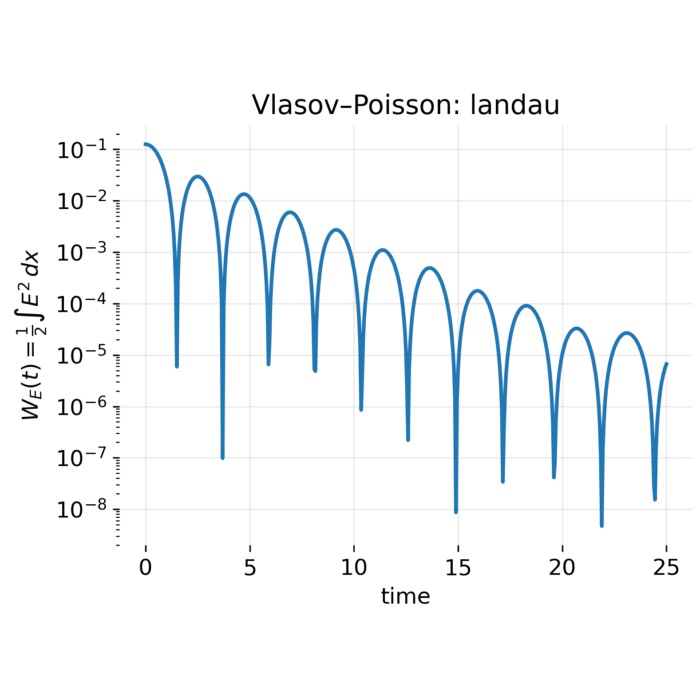
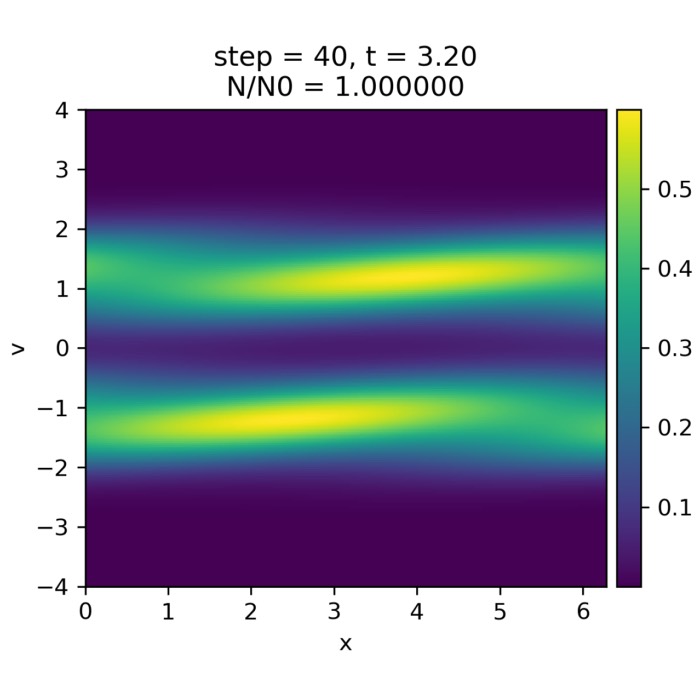
Vlasov–Poisson dynamics: Landau damping and the two-stream instability
The Vlasov–Poisson system provides a minimal kinetic framework to illustrate fundamental plasma processes such as Landau damping and the two-stream instability. By varying the initial velocity distribution, we explore in this post how these inherently kinetic phenomena arise from the same collisionless equations yet lead to qualitatively different macroscopic dynamics.
Kinetic plasma theory: From distribution functions to the Vlasov equation
Kinetic plasma theory describes a plasma as an ensemble of particles represented by a distribution function in phase space. This framework captures velocity space structure, non Maxwellian populations, temperature anisotropies, drifts, beams, loss cones, weak collisionality, resonances, and wave particle interactions. In collisionless space plasmas, the Vlasov equation governs the evolution of the distribution function, providing a self consistent description of plasma dynamics beyond fluid models like magnetohydrodynamics (MHD). In this post, we explore the foundations of kinetic plasma theory, starting from the definition of the distribution function and leading to the Vlasov equation.
Plasma instabilities as dynamical departures from equilibrium
Plasma instabilities mark the transition from passive wave propagation to active energy conversion. While plasma waves describe small amplitude perturbations of a stable equilibrium, instabilities arise when the equilibrium itself is unable to support certain perturbations, leading to exponential growth in time. In mathematical terms, this corresponds to dispersion relations whose solutions acquire a positive imaginary part of the frequency. Physically, instabilities tap free energy stored in gradients, relative flows, or anisotropic particle distributions and convert it into electromagnetic fields and particle motion.
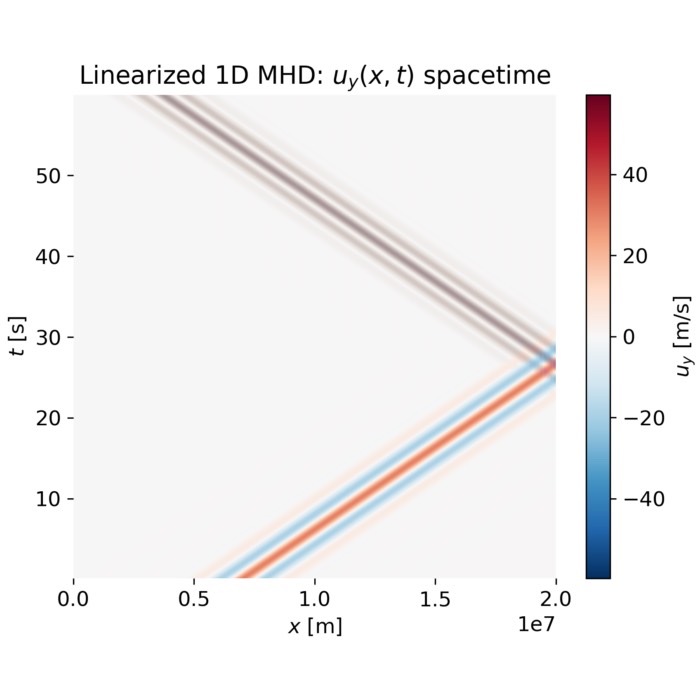
The Alfvén wave as a fundamental mode of magnetized plasmas
Among all plasma waves, the Alfvén wave occupies a special conceptual position. It is the simplest genuinely magnetized plasma mode, arising directly from the coupling between magnetic field line tension and plasma inertia. At the same time, it provides a concrete and analytically tractable example of how collective plasma dynamics interpolate between fluid and kinetic descriptions. In space plasmas, Alfvén waves dominate large scale fluctuations in the solar wind, control energy transport along magnetic field lines, and form the backbone of magnetosphere ionosphere coupling. In this post, we derive the Alfvén wave from first principles, explore its fundamental properties, and discuss its physical interpretation.